Vita vissuta – L'Entropia nell'Universo può solo aumentare

Il telecomando e i suoi codici “segreti”

03/05/202203/05/2022 franzpizzo

SPOILER: Quest’articolo potrebbe essere utile anche a chi vuole clonare il telecomando a infrarossi di un qualunque elettrodomestico, soprattutto nel caso in cui non funzioni con il classico telecomando universale o non sia presente nella lista dei telecomandi delle classiche applicazioni per smartphone!

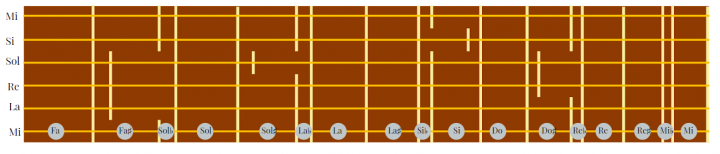
I comuni telecomandi che utilizziamo per cambiare i canali della TV, spegnere e accendere l’aria condizionata gestire le lucine LED inviano dei segnali al dispositivo che comandano attraverso i raggi infrarossi, sono cioè dotati di un LED (una specie di lampadina) in grado di emettere una luce non visibile dall’occhio umano ma che può essere percepita da particolari sensori.

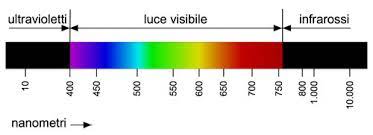
I segnali vengono codificati attraverso una sequenza di accensioni e spegnimenti, il modo con cui questi segnali sono inviati dipende dal protocollo scelto dal produttore dell’apparecchio da comandare. Infatti di protocolli ve ne sono diversi, ma sembra che il più comune sia il protocollo denominato NEC, che è quello che è stato usato in questo caso.

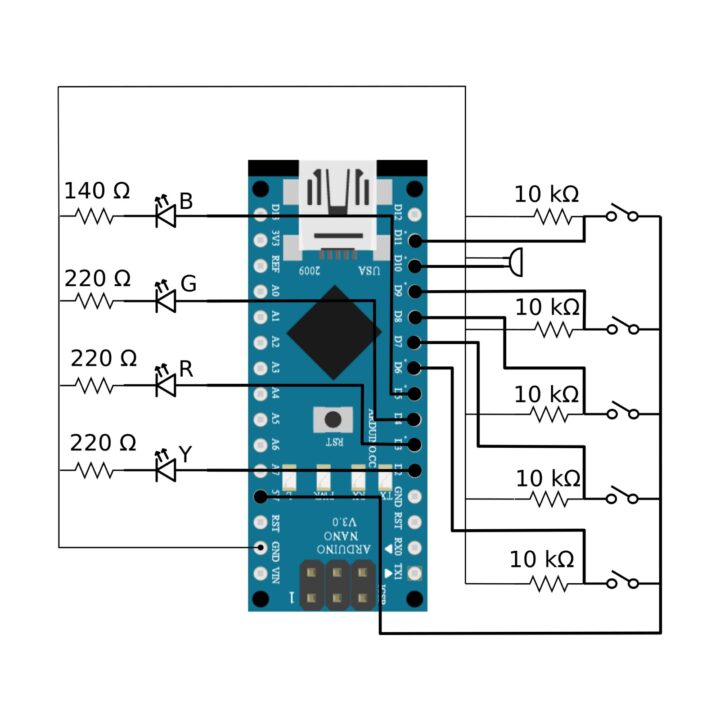
Con un semplice sensore IR collegato al nostro Arduino e con poche righe di codice è possibile visualizzare attraverso il monitor seriale dell’IDE di Arduino i dati inviati dal telecomando.

#include <IRremoteInt.h>
#include <IRremote.h>
int receiver = 2;
IRrecv irrecv(receiver);
decode_results results;
void setup()
{
  Serial.begin(9600);
  irrecv.enableIRIn();
}
void loop()
{
  if (irrecv.decode(&results))
  {
    Serial.print(results.decode_type);    Serial.print("|");
    Serial.print(results.value, HEX);    Serial.print("|");
    Serial.println(results.value, BIN); 
    irrecv.resume();
  }
}

Una volta puntato il telecomando verso il sensore, premendo un tasto qualunque si visualizzano una serie di numeri, come in quest’esempio:

3|FB009A65|11111011000000001001101001100101

La prima cifra chiarisce il tipo di protocollo usato: il 3 sta per protocollo NEC, il 7 invece vale per i telecomandi Samsung e così via. La decodifica completa la trovate nell’header IRremote.h, ed è definita da quest’enum:

typedef enum {
    UNKNOWN = -1,
    UNUSED = 0,
    RC5,
    RC6,
    NEC,
    SONY,
    PANASONIC,
    JVC,
    SAMSUNG,
    WHYNTER,
    AIWA_RC_T501,
    LG,
    SANYO,
    MITSUBISHI,
    DISH,
    SHARP,
    SHARP_ALT,
    DENON,
    LEGO_PF,
    BOSEWAVE,
    MAGIQUEST,
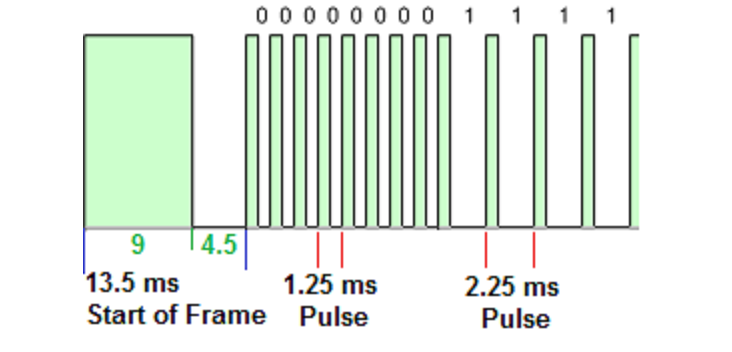
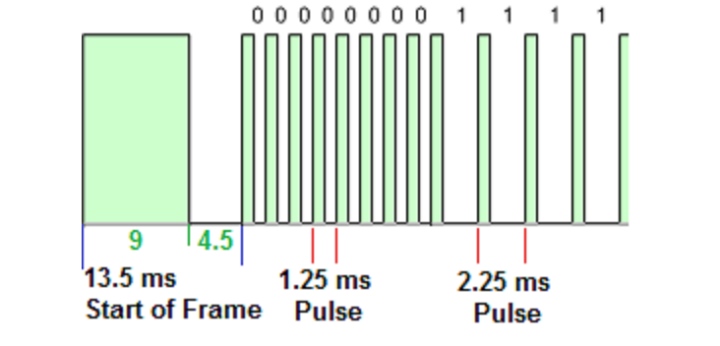
} decode_type_t;

Questi dati sono da interpretare quindi nella codifica NEC. Il protocollo usa una serie di segnali di acceso e spento per codificare le cifre binarie 0 e 1, in un modo che somiglia al codice morse: viene inviato un segnale seguito da una pausa corta (0) o lunga (1).

Vengono quindi inviati due codici, il primo identifica il dispositivo, quindi permette di non inviare all’apparecchio sbagliato il comando. Corrisponde alla prima parte del messaggio ovvero le prime quattro cifre in formato esadecimale (FB00) o le prime 16 se guardiamo al formato binario (1111101100000000) nell’esempio che è stato riportato sopra. Attenzione però questo codice va letto al contrario, cioè 0000000011011111, che trasformato in esadecimale è 00DF (vedi big endian e little endian). Qualunque tasto premiamo sul telecomando questo primo blocco si ripete e quindi solo il dispositivo che lo riconosce esegue il comando inviato nel seguito del messaggio.

I successivi 16 bit equivalgono in realtà ad un messaggio di 8 bit ripetuto due volte, la prima con la codifica binaria usuale, la seconda con i bit invertiti, ovvero con gli 0 al posto di 1 e viceversa, questo si fa evidentemente per intercettare eventuali errori di trasmissione. Quindi la sequenza 1001101001100101 si deve vedere come la coppia di byte 10011010-01100101, che si ottiene invertendo i bit l’una dell’altra, quindi basta considerare solo il primo byte 10011010. Quest’ultimo va letto al contrario, ovvero 01011001, che corrisponde all’esadecimale 59 (l’uso di numeri esadecimali al posto dei decimali in questo contesto è sicuramente più comodo).

A questo punto tutto è pronto, si schiacciano i tasti del telecomando e si prende nota dei codici che vengono mostrati, e in ordine si mettono in un foglio LibreOffice (se volete usate MS Excel, io uso LibreOffice), dove inserisco le formule per codificare il messaggio grezzo: facciamo la prova con il telecomando del vecchio decoder del digitale terrestre 1byOne, cioè di questo:

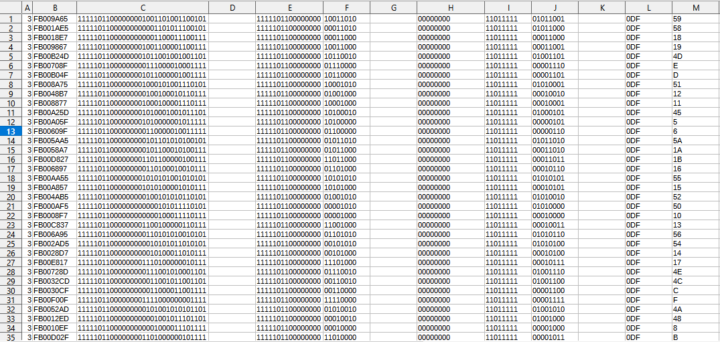
Premo i tasti uno alla volta in ordine dall’alto verso il basso e da sinistra verso destra e ottengo sul monitor seriale tutti i dati che mi servono; ci saranno anche dati sporchi che vanno cancellati e si popolano le colonne A, B e C questo sheet: questi sono i dati grezzi; nelle colonne E e F vanno spacchettati applicando delle formule:

Nella colonna E infatti inserisco questo:

=STRINGA.ESTRAI(C1;1;16)

E nella colonna F

=STRINGA.ESTRAI(C1;17;8)

A questo punto la conversione tra big e little endian con le tre formule rispettivamente nelle colonne H, I e J: non fanno altro che invertire l’ordine dei bit

=STRINGA.ESTRAI(E1;16;1)&STRINGA.ESTRAI(E1;15;1)&STRINGA.ESTRAI(E1;14;1)&STRINGA.ESTRAI(E1;13;1)&STRINGA.ESTRAI(E1;12;1)&STRINGA.ESTRAI(E1;11;1)&STRINGA.ESTRAI(E1;10;1)&STRINGA.ESTRAI(E1;9;1)
=STRINGA.ESTRAI(E1;8;1)&STRINGA.ESTRAI(E1;7;1)&STRINGA.ESTRAI(E1;6;1)&STRINGA.ESTRAI(E1;5;1)&STRINGA.ESTRAI(E1;4;1)&STRINGA.ESTRAI(E1;3;1)&STRINGA.ESTRAI(E1;2;1)&STRINGA.ESTRAI(E1;1;1)
=STRINGA.ESTRAI(F1;8;1)&STRINGA.ESTRAI(F1;7;1)&STRINGA.ESTRAI(F1;6;1)&STRINGA.ESTRAI(F1;5;1)&STRINGA.ESTRAI(F1;4;1)&STRINGA.ESTRAI(F1;3;1)&STRINGA.ESTRAI(F1;2;1)&STRINGA.ESTRAI(F1;1;1)

Infine la conversione in esadecimale nelle colonne L e M:

=BINARIO.HEX(H1)&BINARIO.HEX(I1)
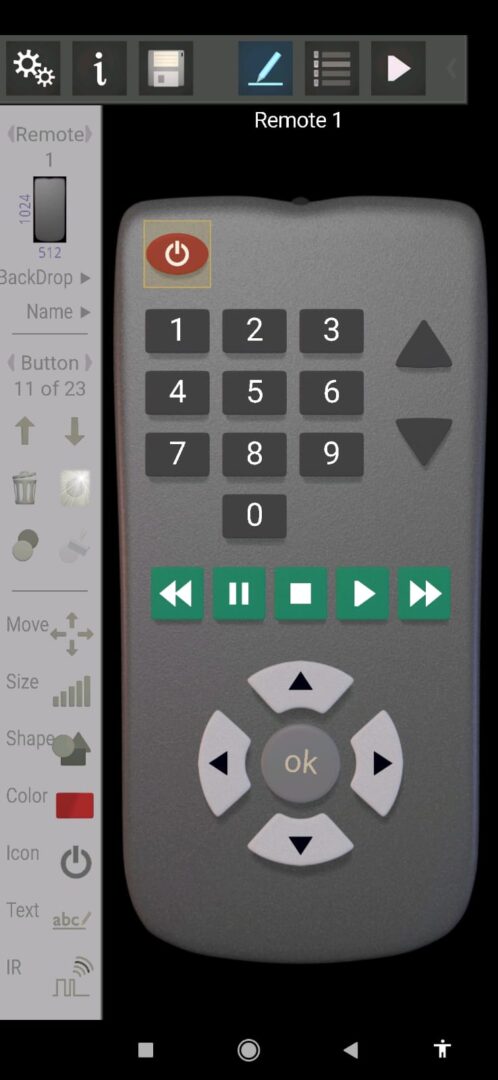
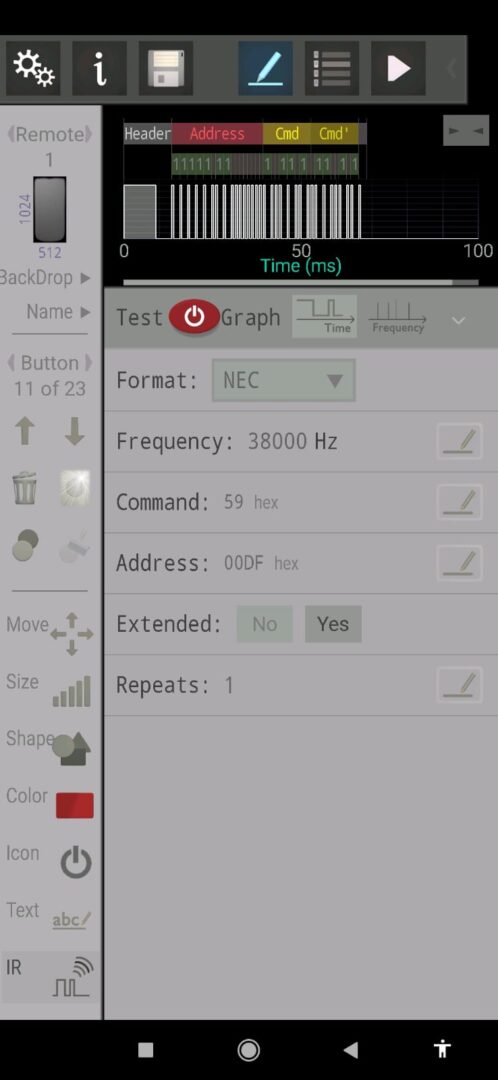
=BINARIO.HEX(J1)

Siamo pronti, abbiamo tutto, dobbiamo solo trovare il modo di sparare i codici, e su questo ci viene incontro una semplice applicazione per Android che su dispositivi compatibili, ovvero i dispositivi che sono dotati di trasmettitore IR, permette di creare un telecomando completamente personalizzabile. L’applicazione è IR Remote Creator e della keuwlsoft che permette di disegnare in maniera completamente libera il telecomando; l’app si presenta così:

Si possono aggiungere o togliere pulsanti cambiare forma e colore di tutto, insomma è un programma completo, e in più ad ogni tasto è possibile associare i codici da inviare via infrarossi, quindi basta copiare i valori calcolati dal foglio LibreOffice:

Con un po’ di pazienza avremo un telecomando perfettamente equivalente a quello di partenza, molto utile nel caso in cui si teme possa rompersi/scomparire misteriosamente il telecomando originale; molti apparecchi come appunto questo 1byOne non presentano alcun tasto sul dispositivo che ne possa permettere l’utilizzo in mancanza del telecomando e trovare il modo di far funzionare un telecomando universale equivale a tentare la fortuna. Invece ecco qua il nostro apparecchio funzionante!

Ciò che abbiamo ottenuto è valido per quest’apparecchio ma l’ho sperimentato anche su altri dispositivi, e sembra funzionare, ma ogni caso è a se, potrebbe cambiare il protocollo o la dimensione del messaggio potrebbe essere a 8 bit piuttosto che a 16 come nel caso che è stato mostrato. Da questo punto di vista l’app è molto flessibile e permette solo di usare gli standard più comuni ma consente di creare pacchetti di messaggi in formati completamente custom,e ciò significa che veramente non ci sono limiti purché ci si armi di pazienza e buona volontà.

Il passatempo dell’estate 2021

07/22/202108/06/2021 franzpizzo

Come ogni estate il tempo libero abbonda e non si sa bene come arrivare a fine giornata senza annoiarsi. Ognuno ha le sue strategie; chi può va in vacanza, ovviamente non tanto per godere del mare e della spiaggia, certo che no, lo scopo è quello di dare un senso a questo vuoto creando delle routine giornaliere che ci impongono di svolgere delle attività: in qualche modo la vacanza ci permette di rimanere in un binario in modo che seppure è chiaro che si perda tempo, tutto ciò è giustificato ed inoltre abbiamo comunque la parvenza di essere indaffarati in qualche tipo di attività.

Ma l’estate è lunga da passare, tre mesi, alla fine ci si annoierà, a meno di non porsi degli obiettivi, dei compiti da svolgere entro la fine dell’estate; ed allora ecco che c’è chi si lancia nello spazio costruendosi un razzo e sparandosi in prima persona (vedi i ricconi Richard Branson, Jeff Bezos che hanno fatto le cose per bene e sono partiti e tornati sulla Terra senza intoppi, emuli di quel Mike Hughes a cui però andò male…) c’è chi legge libri o addirittura pubblica un libro, completa il giornale dei sudoku o si dedica alla ristrutturazione della casa.

Sempre meglio di quelli che si dedicano alle cosiddette “palline clac-clac” che per fortuna non vedo più da qualche estate (ma sono sicuro che torneranno… si ritorneranno… AH-AH-AH! E tu non ci potrai fare nulla! NULLA! AH-AH-AH!

Stiamo parlando quindi di hobby (o per chi conosce meglio la lingua di Shakespeare hobbys), ovvero attività ricreative diverse da quella lavorativa, fatte a volta anche con un reale impegno, come può essere ad esempio scrivere delle amenità su un blog, in generale senza alcun fine di lucro (e in questo caso ci mancherebbe altro).

Un bel passatempo rilassante e alla portata di tutti per esempio è la realizzazione di circuiti guidati da un microcontrollori come Arduino, che possono essere facilmente programmati in linguaggio C: uno spasso insomma. Di progettini da realizzare copiando schemi e codici su blog e pagine web dedicate ce ne sono parecchi, ma è bello dare sfogo alla propria fantasia e immaginazione creando tutto da zero.

L’idea è quella di clonare il gioco del Simon: sono presenti quattro lucette di diversi colori e quattro tasti in corrispondenza. Viene eseguita una sequenza casuale di accensioni e il giocatore deve replicarla. Se ci riesce alla sequenza precedente si aggiunge un nuovo elemento casuale e così via.

Si tratta di un vecchio gioco della Hasbro, in produzione dalla fine degli anni ’70 (del XX secolo) cioè da quando l’elettronica conquistava i primi spazi nell’universo ludico. La realizzazione è semplice perché basta gestire dei diodi led, un cicalino e dei pulsanti. Il microcontrollore usato è l’Arduino nano, molto più piccolo di altri modelli di Arduino e quindi più adatto ad essere usato in dispositivi che hanno anche lo scopo di essere maneggevoli.

Per il diodo led è sufficiente collegare in serie una resistenza adeguatamente dimensionata. Per il led blu è stata usata una resistenza da 140 ohm, mentre per verde, rossa e gialla una da 220 ohm. La resistenza è dimensionata in base alla tensione che assorbe il diodo e tenendo conto che l’intensità di corrente deve rimanere entro determinati limiti, altrimenti si rischia dover buttare il led. La classica formula da applicare è la seguente:

I=\frac{V-V_{led}}{R}

La tensione $V$ è quella in uscita dai pin digitali dell’arduino ed è +5 V, la $V_f$ dipende dal colore, è 3 volt per il blu mentre per rosso, giallo e verde si intorno ai 2 volt; per la precisione rosso 1,8 V, giallo 1,9 V e verde 2,0 V ma poco importa perché le resistenze vanno scelte in modo da avere una corrente al di sotto dei 20 mA.

I pulsanti invece collegano direttamente la tensione con i pin corrispondenti, ma in più in serie aggiungiamo una resistenza da 10 $k\Omega$ verso il GRD. Infine il cicalino (un buzzer passivo) viene aggiunto direttamente tra pin e GRD. Lo schema è essenzialmente questo:

I vari componenti sono abbastanza semplici da inserire nel momento che si comprende lo schema con cui le connessioni si ripetono: l’importante è non fare confusione. Il risultato finale è questo qua:

Quindi abbiamo quattro led di vari colori a cui corrispondono altri quattro pulsanti più un pulsante bianco; il buzzer è il cilindretto nero all’estrema destra. Si tratta in questo momento solo di un hardware spoglio, ovvero senza alcun software che lo gestisca. Il programma di prova che carichiamo funziona perfettamente, quindi andiamo avanti scrivendo un po’ di codice per implementare il gioco: ci serve un generatore di valori casuali che aggiunge ad ogni passo un elemento in una sequenza, visualizzi questa sequenza attraverso l’accensione dei led e controlli che la sequenza replicata dal giocatore corrisponda a quella prevista, insomma un po’ un casino, ma niente di particolare. Il file sorgente è disponibile qui: miniSimon.ino.

Il risultato è illustrato in questo video; ma con lo stesso hardware si potrebbe fare anche di più, si potrebbe immaginare un altro tipo di gioco o altre funzioni; senza cambiare nulla nei collegamenti e modificando solo il codice si può fare tutto quello che la fantasia ci suggerisce; quindi non finisce qui, l’estate è ancora lunga.

[Update]
Infatti non ho impiegato molto tempo per trasformare quest’oggetto in uno strumento musicale: ogni combinazione di tasti produce un tono (nella scala temperata a temperamento equabile, che per chi segue questo blog dovrebbe risultare familiare, altrimenti cliccate qua).

L’associazione tra tasti e note musicali è data dal seguente schema; inoltre premendo il tasto bianco si ottengono le stesse note un’ottava più in alto:

Il codice si può trovare su questo Pastebin; la cosa interessante di questo codice consiste nel modo con cui definisce le frequenze delle note: definito 523 MHz la frequenza del Do, frequenze delle note successive si calcolano moltiplicando più volte per 1,0594…. ovvero per la radice dodicesima di 2, mentre in molti esempi che ho visto in giro le note erano definite da una serie di direttive #define. Il motivo lo trovate nell’articolo già citato.

   frequency[0]=523;
   f=523;
   for(int i=1;i<25;i++){
      f=f*1.0594630943592952646;
      frequency[i]=(int)(f+.5);
   }

Il risultato non è eccezionale, qui un esempio:

Ma adesso spegniamo le luci e…. magia!

Gesù e la pesca miracolosa del numero 153

04/11/202108/05/2021 franzpizzo

Questo articolo tratta nientepopodimeno che di un brano del Vangelo, uno dei libri considerato sacro per un una buona frazione della popolazione umana. Tempo fa, non potendo evitarlo in nessun modo, sono stato ad una funzione religiosa che in alcuni casi è detta anche Messa che, a quanto ho capito è un termine che ha la stessa origine del termine “mensa”: insomma alla fine mangia (infatti dopo abbiamo mangiato). Ogni occasione però può essere buona per imparare qualcosa, e umilmente mi sono messo in ascolto della parola di Giovanni (21: 1-14), che racconta che Simone (alias Petro) e alcuni suoi amici andarono a pescare nel lago di Tiberiade, ma dopo un’estenuante nottata non avevano pescato ancora nulla.

Il vero volto di Gesù: le ricostruzioni moderne basate su metodi scientifici e statistici ci propongono un volto molto diverso dai canoni con cui Gesù è stato rappresentato finora.

Verso l’alba arriva Gesù sulla riva del lago e chiede ai pescatori che si trovavano ad un centinaio di metri dalla riva, se avessero pescato qualcosa, e loro senza riconoscerlo, risposero che non avevano preso proprio nulla! Così Gesù ~~si avvicino alla barca camminando sulle acque~~ pensò di fare qualcosa di utile e ~~fece apparire dei pani e dei pesci affinché tutti potessero sfamarsi~~ disse ai pescatori di buttare le reti sulla destra della barca. Questi ultimi si fidarono e furono subito ricompensati perché a fatica riuscirono a sollevare la rete dall’acqua talmente essa era piena!

Mentre trascinavano la rete a riva Gesù aveva già preparato la brace: disse loro Gesù: «Portate un po’ del pesce che avete preso or ora». Insomma fecero una bella grigliata per colazione! Probabilmente all’epoca era normale, dal momento che non era ancora stato inventato il cappuccino con il cornetto. Prima di cucinarli contarono i pesci (perché mai li hanno contati non si sa) e nel passo è sottolineato che i pesci fossero centocinquantatré. Se finora la storia sembra strana possiamo aggiungere che tutto questo avveniva quando ormai Gesù era morto!

Ebbene a parte tutta la simbologia legata al lago, alla pesca, la rete, il lato destro della barca ecc. quello che mi ha colpito il i numero di pesci: 153. Perché proprio questo numero; sarebbe bastato dire che c’erano più di cento pesci per far capire che ne avevano preso una quantità abbondantissima, invece si è puntualizzato, e questo è strano.

Gli ebrei non erano un popolo di grandi matematici, come potevano essere i babilonesi o i greci, non erano particolarmente interessati alla geometria, non avevano grosse basi di aritmetica ma a loro i numeri interessavano molto! Per loro la parola era importante, anche la parola scritta, e i numeri erano in stretta relazione con la parola perché il sistema di numerazione ebraico prevedeva l’uso dei simboli del loro alfabeto per rappresentare anche i numeri oltre che le parole.

1	א	aleph	10	י	yud	100	ק	quf
2	ב	beit	20	כ	khaf	200	ר	resh
3	ג	ghimel	30	ל	lamed	300	ש	shin
4	ד	dalet	40	ם	mem	400	ת	tav
5	ה	hey	50	נ	nun	500	ך	khaf sofit
6	ו	vav	60	ס	samekh	600	ם	mem sofit
7	ז	zain	70	ע	‘ain	700	ן	nun sofit
8	ח	cheit	80	פ	peh	800	ף	peh sofit
9	ט	tet	90	צ	tzadde	900	ץ	tzadde sofit

Sistema di numerazione ebraico

Basta quindi giustapporre questi caratteri per ottenere qualcosa che si può interpretare come parola o come numero (ovviamente si legge nell’ordine opposto a quello che usiamo noi). I numeri seguono una logica additiva, così כלב che in ebraico significa cane è anche il numero 2+30+20=52, e al contrario un numero poteva rappresentare o addirittura evocare qualcosa: stiamo parlando della Cabala Ebraica, argomento di cui non conosco assolutamente nulla per cui evito di dire sciocchezze chiudendo qui il discorso, ma ricordando che è un argomento studiato da millenni e che la Bibbia è piena di riferimenti cabalistici.

Il nostro 153 contiene probabilmente riferimenti cabalistici che chiariscono il significato metaforico della pesca abbondante (su questo non mi dilungo), ma è interessante anche motivi prettamente numerici, e ciò fa pensare che il 153 non è un numero scelto a caso.

Di Albrecht Dürer – Sconosciuta, Pubblico dominio, Collegamento

Il numero 153 non è un numero primo (questo lo avrebbe dato una connotazione matematicamente interessante), è quindi un numero composto: 153=3² x 17. Sembrerebbe una cosa abbastanza banale, ma a ben guardare 3² = 3 x 3 ovvero una griglia di 3 quadrati per ogni lato che ricorda un quadrato magico o se vogliamo anche il gioco del sudoku. In questa griglia (una rete come quella per prendere i pesci o come la graticola usata per cucinarli) inseriamo il numero 17 in ogni riquadro libero, la somma è 153 (ovviamente): quadrati magici, magia, cabala, esoterismo, la situazione si fa interessante…

Osserviamo che il numero 153 ha interessanti proprietà: ad esempio è un numero triangolare! Spieghiamo cosa significa: è un numero dato dalla somma di un certo numero di interi consecutivi: 6=1+2+3 quindi 6 è un numero triangolare.

I numeri triangolari sono 1, 3, 6, 10, 15, 21, 28, ecc… e sono tutti quelli che si possono scrivere nella forma (n+1)n/2 e hanno questo nome perché… basta vedere il disegno. Anche 153 è quindi triangolare, infatti:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 + 17 = 153

Ed è spuntato (per caso?… non credo) ancora una volta il numero 17! Ed ora: Abracadabra!

Il 153 è anche un numero esagonale, un numero del tipo (2n² – n): fanno parte della sequenza 1, 6, 15, 28, 45, 66, 91, 120, il nostro 153, 190 e tanti altri… e si chiamano esagonali perché…

Ma possiamo tranquillamente continuare: probabilmente non tutti sanno che il punto esclamativo è usato anche per indicare un’operazione matematica: il fattoriale. Ad esempio con 5! si rappresenta il prodotto 1 x 2 x 3 x 4 x 5, per cui 5! = 120 ovvero è il prodotto di tutti gli interi fino al numero stesso. Facendo un po’ di conti è facile scoprire che 1! + 2! + 3! + 4! + 5! =153.

Cosa si può dire riguardo le cifre di 153? Se di considerano i cubi delle cifre e le si sommano 1³+5³+3³=… lo devo pure dire? Non lo indovinate? È proprio 153 e ciò fa di lui un numero narcisista (non è un appellativo messo a caso, è il termine matematico con cui si definisce questa classe di numeri).

Lasciando da parte le relazioni aritmetiche illustrate (senza contare quelle non illustrate) passiamo alla valenza geometrica del 153. Consideriamo due circonferenze dello stesso raggio fatte in modo che il centro dell’una passi per la circonferenza dell’altra. I punti A e B sono i centri, C ed D sono le intersezioni tra le due circonferenze ed il segmento AB interseca CD nel punto E. È facile notare che ABC è un triangolo equilatero e pertanto è si ricava che EC=√3/2 AB.

In sostanza il rapporto CD/AB è √3 (o se vogliamo, fatto 1 il raggio AB, il segmento DC è √3). Ma fin dall’antichità √3 è stato approssimato dal rapporto 265/153 (con la calcolatrice potete facilmente trovare che (265/153)²=2.9999… praticamente 3). Questa certo è un’ulteriore strana coincidenza, ma…

Questo simbolo (in rosso) rappresenta un pesce (in fondo siamo partiti dai pesci) ed è il più antico simbolo della cristianità e al suo interno c’è il 153!

Tutto molto bello, intanto la messa è finita, ho imparato qualcosa e me ne posso andare in pace contento perché almeno non ho perso il mio tempo.

Costruzione matematica della scala pitagorica

06/23/201906/04/2021 franzpizzo

I moderni strumenti musicali producono una serie di note codificate in base a criteri che hanno avuto una interessante evoluzione nel corso dei secoli.

Oggi sappiamo il suono è un’onda trasmessa in un mezzo, caratterizzata quindi da intensità, lunghezza d’onda e frequenza nonché dalla propria forma d’onda. L’immagine che segue rappresenta un’onda sinusoidale, che si può descrivere cioè tramite la funzione trigonometrica seno. Ma la forma dell’onda può anche essere diversa, ad esempio quadra o triangolare. Il suono prodotto avrà una differente connotazione.

La caratteristica dell’onda che ci interessa in questo caso è la frequenza, ovvero il numero di oscillazioni che l’onda effettua in un secondo (1 Hz =1 ciclo/s). Ad onde con differente frequenza corrispondono differenti percezioni uditive. Le note più gravi hanno una frequenza bassa, quanto tanto più sono acute tanto più la frequenza sarà alta. La corrispondenza tra nota e frequenza è stata codificata per la prima volta da Pitagora nel VI secolo a.C. in maniera analoga a quanto esposto di seguito.

Una corda posta in tensione e fatta vibrare produce un suono. Egli studiò il modo con cui i suoni variano a mano a mano che si riduce la lunghezza della corda: la frequenza con cui la corda vibra aumenta quando la corda viene accorciata e i suoni ottenuti risultano più acuti. Si può notare che il suono prodotto da una corda completamente estesa confrontato con il suono dalla stessa corda ridotta alla metà risulta sovrapponibile benché diverso. Ciò è dovuto al fatto che dimezzando la lunghezza della corda la sua frequenza si raddoppia: le due onde sonore hanno forme strettamente correlate.

In questo caso si dice che i suoni prodotti dalle due corde hanno la distanza di una ottava. Nella notazione moderna le note che distano un’ottava hanno lo stesso nome, infatti entrambe le note di seguito rappresentate sono chiamate Do.

Ottava

Raddoppiando o dimezzando la frequenza di una nota si produce la stessa nota trasposta di un’ottava.

Due suoni prodotti in sequenza possono dare un effetto “gradevole” o “sgradevole” all’orecchio umano.
Tra i vari abbinamenti possibili Pitagora notò che riducendo la corda ad $\frac{1}{3}$ o, il che è lo stesso, ai $\frac{2}{3}$ (suonando cioè la nota un ottavo superiore), la nota prodotta risulta “gradevolmente abbinata” alla prima nota.

Il rapporto tra le frequenze di queste due note è 3:2, l’inverso del rapporto tra le lunghezze delle corde.
Ciò rende ragione della sensazione di “giusto abbinamento”: ogni due oscillazioni della prima corda la seconda oscilla 3 volte.

La nota separata dalla prima da un rapporto tra le frequenze di $\frac{3}{2}$ viene detta quinta giusta.

Quinta

Moltiplicando per $\frac{3}{2}$ (o per $\frac{2}{3}$ ) la frequenza di una nota si produce una nota che “si abbina bene” con la prima.

Mediante un procedimento matematico si individuano i rapporti che corrispondono a nuove frequenze. Proseguendo di quinta in quinta si ottiene una sequenza di note che “suonano bene insieme”. La prima nota è in rapporto 1:1 con se stessa, la seconda è 3:2 della prima. Individuiamo una nuova nota in modo che abbia un rapporto 3:2 con quest’ultima; poiché $\frac{3}{2}$ × $\frac{3}{2}$ = $\frac{9}{4}$ , essa è in rapporto 9:4 con la prima.
Poiché $\frac{9}{4} > 2$ questa nota ha superato l’ottava della nota base; riportiamola quindi nell’ambito della prima ottava dividendo la frazione per 2:

$\frac{9}{4}$ × $\frac{1}{2}$ = $\frac{9}{8}$ .

Otteniamo quindi un suono con un rapporto di frequenza 9:8 rispetto alla nota di riferimento.

Cerchiamo adesso la quinta del suono 9:8 moltiplicando questo rapporto per $\frac{3}{2}$ e otteniamo 27:16.
La successiva è $\frac{27}{16}$ × $\frac{3}{2}$ =81:32. Anche quest’ultima frazione rappresenta una nota esterna all’ottava, per cui va divisa per 2, ottenendo 81:64. L’ultimo rapporto sarà $\frac{81}{64}$ × $\frac{3}{2}$ = 243:128.
Aggiungiamo infine il suono la cui quinta è 1:1, invertiamo cioè il calcolo ottenendo la nota 2:3, infatti la quinta di 2:3 è $\frac{2}{3}$ × $\frac{3}{2}$ = 1.
Questa nota va riportata anch’essa nella giusta ottava moltiplicandola 2 e ottenendo infine 4:3.
Questo procedimento ha generato la sequenza di rapporti:

1:1, 3:2, 9:8, 27:16, 81:64, 243:128, 4:3

che ordinanti in senso crescente diventano

1:1, 9:8, 81:64, 4:3, 3:2, 27:16, 243:128

A queste note associamo convenzionalmente dei nomi, che per tradizione sono nell’ordine Do, Re, Mi, Fa, Sol, La, Si.

Il rapporto tra due note successive è $\frac{9}{8}$ tranne che tra Fa e Mi e tra Si e Do per i quali è $\frac{256}{243}$ . Il primo intervallo è detto tono, mentre il secondo è il semitono.

La scala musicale così ottenuta può essere ampliata aggiungendo un suono tra le note separate da un tono.
Ad esempio dal Do si può passare al Do♯ aggiungendo un semitono ovvero $\frac{256}{243}$ . Il Do♯ sarà rappresentato quindi dalla frazione 1 × $\frac{256}{243}$ = $\frac{256}{243}$ .
A sua volta il Re♯ si otterrà da $\frac{9}{8}$ × $\frac{256}{243}$ = $\frac{2304}{1944}$ = $\frac{32}{27}$ . In conclusione:
Do♯ = 1 × $\frac{256}{243}$ = $\frac{256}{243}$
Re♯ = $\frac{9}{8}$ × $\frac{256}{243}$ = $\frac{32}{27}$
Fa♯ = $\frac{4}{3}$ × $\frac{256}{243}$ = $\frac{1024}{729}$
Sol♯ = $\frac{3}{2}$ × $\frac{256}{243}$ = $\frac{128}{81}$
La♯ = $\frac{27}{16}$ × $\frac{256}{243}$ = $\frac{16}{9}$ .

Si può notare che spostarsi di due semitoni non equivale a spostarsi di un tono, infatti se dal Re ci si sposta di un semitono all’indietro si ottiene ( $\frac{9}{8}$ )/( $\frac{256}{243}$ )= $\frac{2187}{2048}$ .
Questa nota, diversa dal Do♯, è detta Re♭.

Tra il Do♯ e il Re♭ vi è una distanza di ( $\frac{2187}{2048}$ )/( $\frac{256}{243}$ )= $\frac{531441}{524288}$ ≅ 1,0136.
Tale intervallo è il cosiddetto comma pitagorico, che seppure sia piccolo è apprezzabile dall’orecchio umano.

Le seguenti note completano la scala cromatica:
Re♭ = ( $\frac{9}{8}$ )/( $\frac{256}{243}$ ) = $\frac{2187}{2048}$
Mi♭ = ( $\frac{81}{64}$ )/( $\frac{256}{243}$ ) = $\frac{19683}{16384}$
Sol♭ = ( $\frac{3}{2}$ )/( $\frac{256}{243}$ ) = $\frac{729}{512}$
La♭ = ( $\frac{27}{16}$ )/( $\frac{256}{243}$ ) = $\frac{6561}{4096}$
Si♭ = ( $\frac{243}{128}$ )/( $\frac{256}{243}$ ) = $\frac{59049}{32768}$

Questa è la rappresentazione delle note sul pentagramma: il numero di note della scala pitagorica cromatica è 17.
In passato sono stati costruiti strumenti che rispettano la scala pitagorica. Per noi hanno un aspetto poco usuale.

Ricostruzione del clavicembalo cromatico di Carlo Gesualdo da Venosa
esposto al Museo del Castello di Gesualdo

In questo ipotetico manico di chitarra sono rappresentate le posizioni corrispondenti alla scala cromatica pitagorica

Per evitare questi e altri inconvenienti nei secoli si sono ideate altre scale, fino ad arrivare al temperamento equabile:

è stato annullato il comma pitagorico: Do♯ e il Re♭ coincidono
tra due semitoni vi è un rapporto costante, i suoni ottenuti sono prossimi ai suoni della scala pitagorica
le note della scala cromatica sono ridotte a 12

Poiché si richiede che tra due semitoni il rapporto sia costante e che le note distanti un’ottava abbiano un rapporto pari a 2, il rapporto costante tra i semitoni deve essere un numero k tale che
k¹² = 2 cioè k=¹²√2 ≈ 1,05946.

Posto k=¹²√2 ≈ 1,05946, si può notare che questa quantità è molto prossima al rapporto $\frac{256}{243}$ ≈ 1,0535 che contraddistingue la distanza tra Si e Do e tra Mi e Fa nella scala pitagorica.
Inoltre k² ≈ 1,12246 risulta una buona approssimazione del rapporto $\frac{9}{8}$ = 1,125 cioè l’ampiezza di un tono.

Noto già nell’antichità (Aristosseno di Taranto intorno al 320 a.C.), questo tipo di temperamento ha impiegato secoli prima di essere accettato, anche per la presenza del fattore irrazionale ¹²√2.
L’aspetto della tradizionale tastiera del pianoforte è data dalla scala così costruita

Sol

Do1

¹²√2

(¹²√2)²

(¹²√2)³

(¹²√2)⁴

(¹²√2)⁵

(¹²√2)⁶

(¹²√2)⁷

(¹²√2)⁸

(¹²√2)⁹

(¹²√2)¹⁰

(¹²√2)¹¹

(¹²√2)¹²

La tastiera della chitarra tradizionale confrontata con un’ipotetica chitarra in scala pitagorica rende maggiormente l’idea di cosa si intenda per temperamento equabile. Le posizioni sulla prima sono una buona approssimazione dei corrispondenti sulla seconda, e così anche i suoni che si ottengono.

The Distracted Mind

06/03/201806/03/2018 franzpizzo

E già per fare sta stronzata c’ho perso la prima mezz’ora della giornata, ma adesso basta: “libera il Marzullo che è in te”!

Il Forerunner 110 e il suo cinturino

02/10/201802/10/2018 franzpizzo

Era all’incirca il luglio del 2011 quando ho deciso di comprarlo. Ho preso questo modello perché tutti gli altri modelli in circolazione erano ingombranti patacconi. Il Forerunner 110 della Garmin superava di poco le dimensioni di un normale orologio. Risultava pertanto comodo da portare durante la corsa o anche durante la giornata.
Il difetto era evidente, ma l’ho trascurato. Sicuramente non mi pento di aver comprato questo modello, ma dopo qualche anno ho dovuto trovare il modo di utilizzare un orologio con il cinturino rotto.
Il difetto consiste appunto nel fatto che il cinturino fa corpo unico con l’orologio e non è possibile sostituirlo con un cinturino standard o adattarne uno.
All’inizio quindi con della colla, poi dello spago e dello scotch. Alla fine non c’è stato nulla da fare il cinturino è andato in mille pezzi.

Si potrebbe pensare ad un caso di obsolescenza programmata: il cinturino di qualunque orologio, soprattutto se di plastica, ha una vita limitata mentre comprare un cinturino della Garmin… ne vogliamo parlare? No non ne parliamo.
Potremmo invece comprare un nuovo orologio con GPS? Forse questa sarebbe una buona idea, ma finché è possibile fare a meno di un upgrade tecnologico, a mio parere, si può aspettare almeno fino a quando non vengono messi sul mercato prodotti di tecnologicamente più maturi. C’è invece chi rincorre continuamente la tecnologia: ognuno faccia come crede.
E quindi dopo aver cercato e confrontato le soluzioni di altri sventurati, e riflettendo su come risolvere la situazione ho trovato una strada tutta mia.
Materiali occorrenti

Cinturino in tessuto da pochi euro
bustina porta CD (ne ho una collezione)
stringhe chiudisacchetti

La bustina del CD va ragliata in modo che non risulti troppo grande, la si può tagliare anche alla fine dopo aver regolato la dimensione.

Si inserisce l’orologio nella bustina

La si appoggia sul cinturino

Si chiude il tutto con le stringhe

Ed ecco un antiestetico-ma-di-nuovo-funzionante Garmin Forerunner 110

Antiestetico: sicuramente; si potrebbero usare delle stringhe di colore nero, l’effetto migliorerebbe.
Di nuovo funzionante: sicuramente, la plastica non dà alcun problema, magari sono io ad essere poco sensibile, ma almeno per il momento non mi irritato il polso né posso dire di avere avuto problemi nella traspirazione (del polso).
Leggibile: un po’ di meno dell’originale, a volte riscontro qualche riflesso.
Usabile: i tasti rimangono comunque accessibili, basta fare un minimo di attenzione riguardo a come si posizione la bustina.

Chi bussa a questa porta? E a quest’ora!?

08/07/201701/22/2018 franzpizzo

Non ti aspetteresti mai sentire bussare al citofono intorno alle 15.30, soprattutto il 7 di agosto. Eppure questo 7 agosto, alle ore 15.30 circa ecco che suona il citofono.
Di pomeriggio in genere sono comunque attivo, ho solo un breve momento di mancamento dovuto al sangue che accorre allo stomaco per la digestione e di conseguenza il cervello ne rimane privo.
In tutte le culture questo momento è noto e definito da termini precisi: da noi è detto “controra”, ma potrebbe anche essere indicato con termini più tecnici come “coma digestivo” oppure “nummrumpitocazz”.
Cercando di riprendermi dal brusco risveglio e rispondo al citofono: comunicazioni dell’ENEL. Ho capito già tutto, ma sono una persona curiosa e mi interessa capire quale faccia da disperato può avere uno che alle 15.30 del 7 agosto, temperatura misurata 38° C, temperatura percepita 45° C, gira per le strade di un infimo paesino di provincia a procacciare clienti.
Esco in cortile, e mi rendo conto che sono abbigliato in maniera perfetta per una pennichella sul divano di casa propria, ma non per presentarsi ad un estraneo, ma penso “masticazzichisenefrega”: lo voglio vedere, voglio guardarlo in faccia a tutti i costi.
Finalmente eccolo, giovane, avrà avuto appena 18 anni, perfetto nel suo completo giacca e cravatta, l’unico che ha, comprata apposta per festeggiare il suo recente 18° compleanno: auguri!
Si proteggeva dal sole cercando riparo dal muretto, rosso in faccia, giacca e cravatta, il 7 agosto alle ore 15.30, con una temperatura misurata 38° C all’ombra, al sole saranno stati almeno 50. Con lui un ragazzina che stava patendo allo stesso modo: che bello essere giovani, nessuno ti ferma, può piovere o fare caldo, resisti a qualunque cosa. Beata gioventù!
Mi istruisce sul fatto che è necessario passare al mercato libero, e chiede di vedere la mia ultima fattura dell’enel per controllare un codice. Se corrisponde posso avere uno sconto del 30%.
Non ho voluto infierire, sono stato gentile quando l’ho scacciato.
Per i giovani venditori porta a porta dell’enel (enel energia o quello che è) una prece.

È solo una questione di Logica

07/16/201607/16/2016 franzpizzo

Gli argomenti di logica matematica che più solleticano la fantasia sono quelli che sembrano andare contro il senso comune. Tra questi il caso più interessante e ricco di spunti è la descrizione del significato dell’implicazione logica.
L’implicazione è un operatore che si applica a due frasi valide; il risultato è una terza frase, composta dalle prime due che avrà una struttura del tipo “se … allora …” e sarà anch’essa una frase valida.
Ho usato qui il termine “frase valida” in maniera impropria per evitare di usare il termine più corretto ma trippo “pomposo” di formula ben formata (tanto che in genere per essa si usa l’abbreviazione fbf), che, sempre per semplificare, si può definire come una frase che assume uno e uno solo dei valori tra vero e falso.
Dal punto di vista più formale, siano A e B due frasi valide, applicando l’implicazione logica otteniamo la frase valida “se A allora B“, che se spesso si può trovare nella forma “A è condizione sufficiente per B” o “B è condizione necessaria per A“, o ancora, utilizzando la simbologia A[math]\implies[/math]B. Al pari di A e B anche A[math]\implies[/math]B, in quanto frase valida, sarà vera o falsa. In particolare sarà sempre vera tranne nel caso in cui A è vera e B falsa.
Per chiarire la definizione di un operatore logico (per chi non lo sa, ce ne sono altri oltre l’implicazione) si usa spesso la tavola della verità, cioè si enumerano tutte le possibili combinazioni di valori di verità di A e B e si indica il corrispondente valore della frase composta:

A	B	A[math]\implies[/math]B
V	V	V
V	F	F
F	V	V
F	F	V

In Matematica, e a maggior ragione in Logica Matematica, una definizione non si discute ma la si tratta come una pura convenzione. Aver chiamato quest’operatore implicazione e leggerla come “se A allora B” non significa ad esempio che tra A e B ci sia una relazione di causa-effetto, ed in generale non bisogna farsi trarre in inganno dal significato che una frase del genere ha nel “linguaggio comune”.
Per chiarire ciò caliamo questo discorso in un caso reale; può capitare ad esempio di essere impiegato presso una società (che per esempio può essere una qualunque società di consulenza informatica o quant’altro) per diversi anni e con il tempo trovarsi ad essere relegato in attività sempre più marginali, ad avere sempre meno credito e di conseguenza ottenere delle valutazioni di anno in anno peggiori malgrado si cerchi di contribuire con il proprio impegno e disponibilità (sì, in queste società alla fine dell’anno ti fanno una pagellina, proprio come a scuola, eppure quello che fai è un lavoro e sei inquadrato con un Contratto Collettivo Nazionale). Ci si può chiedere per quale motivo continuare nell’impegnarsi a contribuire al successo del progetto per cui si lavora e in generale per l’azienda, dal momento che non si si otterrà nulla in cambio? Per essere chiari lavorare sì e con impegno, perché è ciò per cui è pagati ed è tuo dovere rispettare l’impegno contrattuale; ma tutto ciò che è extra? Perché essere disposti a dare di più?
La domanda è fondamentale, ma quello che conta soprattutto è la risposta: “se questa società durerà a lungo allora impegnati quanto più è possibile”.
Abbiamo una frase del tipo “se A allora B“, dove:

A=”questa società durerà a lungo”;

B=”impegnati quanto più è possibile”.

Ogni frase ha la sua negazione, cioè una frase valida che è vera se la frase di partenza è falsa e falsa se la frase di partenza è vera:

[math]\neg[/math]A=”questa società non durerà molto”

[math]\neg[/math]B=”impegnati solo il necessario”

Sottolineiamo qui la prima considerazione controintuitiva: la frase A [math]\implies[/math]B non equivale a [math]\neg[/math]A [math]\implies[/math][math]\neg[/math]B: non è corretto dire “se questa società non durerà molto allora impegnati solo il necessario”, bensì la frase corretta deve essere scritta “se impegnati solo il necessario allora questa società non durerà molto”. La cosiddetta forma contronominale dell’implicazione assume la forma [math]\neg[/math]B [math]\implies[/math][math]\neg[/math]A.

Una seconda considerazione riguarda la stessa definizione di implicazione: questa frase è sempre vera a meno che A sia vera e B falsa. Aiutandoci anche con la tabella precedente si ha che l’implicazione è vera nei seguenti casi:

“questa società durerà a lungo” è vera e “impegnati quanto più è possibile” è vera
“questa società durerà a lungo” è falsa e “impegnati quanto più è possibile” è vera
“questa società durerà a lungo” è falsa e “impegnati quanto più è possibile” è falsa

mentre è falsa nel caso

“questa società durerà a lungo” è vera e “impegnati quanto più è possibile” è falsa

Riscrivendo le frasi in forma negativa, le frasi atomiche sono vere ed è vera anche l’implicazione:

“questa società durerà a lungo” e “impegnati quanto più è possibile”
“questa società non durerà molto” e “impegnati quanto più è possibile”
“questa società non durerà molto” e “impegnati solo il necessario”

mentre in questo caso, malgrado le frasi atomiche siano vere, l’implicazione è falsa:

“questa società durerà a lungo” e “impegnati solo il necessario”

In primo luogo, supponendo l’implicazione vera, si nota che B sia vero o meno non ci permette di dire nulla sul valore di verità di A, dal momento che “impegnati quanto più è possibile” è vera, non è detto che sia vero o che “questa società durerà a lungo”, ma lo stesso avviene se “impegnati solo il necessario” è vera: “questa società durerà a lungo” può essere vera o falsa.
A rafforzare tale stranezza tra A e B c’è solo una relazione logica e non una relazione di causa-effetto: “questa società non durerà molto” è causa del fatto che devi “impegnati quanto più è possibile”? Come abbiamo detto la risposta è no.

Un’altra considerazione sull’implicazione consiste nella possibilità di essere scritto in forme alternative completamente equivalenti, ottenendo cioè la stessa tabella di verità. La scrittura alternativa dell’implicazione è [math]\neg[/math]A [math]\lor[/math]B: quest’ultima assume gli stessi valori di verità di A [math]\implies[/math]B, ciò vuol dire che l’implicazione equivale alla frase “questa società non durerà molto o impegnati quanto più è possibile”, che non ha molta relazione con quanto il senso comune ci suggerisce.

Spero che l’aver inspirato abbastanza dubbi, nella speranza di indurre chi legge ad approfondire ma una cosa la posso svelare; per quanto mi riguarda [math]\neg[/math]B (“impegnati solo il necessario”) è quanto ho fatto dal momento che ho realizzato che impegno e disponibilità non corrispondeva nessun tipo di gratificazione, anzi sembrava che avvenisse il contrario; altresì dal momento stavo solo aspettando il momento giusto per cambiare lavoro, cosa che era ormai nell’aria, ho dovuto solo pazientare un po’.

3.14.15 Giorno del Pi-Greco del Secolo

03/14/201502/19/2021 franzpizzo

Il giorno del pi-greco ricorre ogni anno il 14 marzo, che scritto in formato americano si indica appunto con 3.14. Quest’anno il giorno del pi-greco sarà ancora particolare, perché le cifre dell’anno formano in numero 3.1415: sarà il giorno del pi-greco del secolo!

Ogni anno creo un evento su Facebook e per attirare l’attenzione cerco di mettere in evidenza delle curiosità, quest’anno il tema è “Pi-Greco e Simpson. Quale relazione ci può essere tra le due cose?”

Forse nessuna, ma cercando su internet ci si può imbattere in questa strana formula matematica, e allora qualcosa sotto c’è:

Si tratta di un metodo di integrazione, ci serve una funzione da integrare; il risultato potrebbe servirci per approssimare pi-greco. L’idea più immediata potrebbe essere quella di integrare $\sqrt{1 + x^2}$ tra 0 e 1 (area del settore circolare nel 1° quadrante), tenendo conto che l’area del cerchio di raggio 1 è proprio pi-greco, basterà moltiplicare il risultato per 4. Io però eviterai di usare questa funzione, comunque presenta un radicale e si dovrebbe trovare il modo di calcolare la radice, introducendo un ulteriore problema nel problema: evitiamo prendendo una funzione diversa, ma quale?
Precisiamo, giusto per non creare spiacevoli equivoci, la formula di integrazione presentata non è di Homer Simpson, ma prende il nome da Thomas Simpson, anche se la formula era già nota ai suoi tempi. Non è improbabile però che gli autori della serie di cartoni (tutti con competenze e studi scientifici) abbiano dato di proposito al protagonista il cognome del famoso matematico. Famosi sono inoltre i riferimenti matematici, espliciti e nascosti, presenti negli episodi.
Una bella funzione razionale è $f(x)=\frac{1}{1 + x^2}$ , e fa proprio al caso nostro; integrata tra 0 e 1 dà $arctg(1)$ che corrisponde all’angolo di 45°, perché come ben noto (?) $tg(45^{\circ})=1$ . Ma l’angolo di 45° è proprio $\pi/4$ .
Abbiamo quindi una funzione facile da calcolare e da inserire nella formula di Simpson: andiamo avanti senza indugi al calcolo di pi greco!
Per essere più chiari, useremo la suddetta formula di Simpson (meglio nota come Regola di Cavalieri-Simpson) per calcolare in maniera approssimata quest’integrale.
$\int_{0}^{1} \frac{1}{1 + x^2} dx = \frac{\pi}{4}$ .
Ovviamente non proveremo a calcolarlo manualmente: abbiamo il computer e un bellissimo ambiente di programmazione tra l’altro gratuito e facile. Non ci resta che scrivere (anzi comporre in questo caso) il programmino ed è fatta.

Il calendario perpetuo di Conway

01/10/201508/21/2020 franzpizzo

Non dovrebbe essere necessario presentare un personaggio come John H. Conway, uno dei più famosi e importanti matematici viventi [quando è stato scritto l’articolo, chi legge ora saprà che della sua morte a causa del coronavirus avvenuta nel 2020, ndr], ma ho notato invece che è necessario presentarlo.
Oltre ad aver raggiunto una fama mondiale nel campo della matematica è famoso anche per il suo carattere estroso e anticonvenzionale. È stato attivo nella ricerca sulla Teoria dei Gruppi, ha contribuito allo studio del cosiddetto “Gruppo Mostro” e alla classificazione dei gruppi semplici finiti, realizzando il famoso Atlante[1].
Il suo carattere lo ha portato a interessarsi di vari e particolari aspetti della matematica ad esempio a sviluppare ricerche in ambiti ludici: dall’analisi di giochi classici all’invenzione di nuovi giochi.

Può essere sicuramente definito un genio, ma non di quelli che preferiscono isolarsi dal mondo per pensare solo al suo lavoro; al contrario Conway è una persona estremamente estroversa a cui piace anche mettere in mostra la propria intelligenza, l’eccezionale memoria, la capacità di effettuare calcoli e arrotolare in vari modi la sua lingua[2].

Tra le sue particolari “invenzioni” vi è la creazione di un algoritmo/metodo mnemonico per conoscere il giorno della settimana di qualunque data.
Il calcolo è abbastanza semplice, dal momento che ogni anno è caratterizzato da un o specifico giorno della settimana, detto doomsday; ad esempio nell’anno 2000 il doomsday era il martedì, nel 2001 il mercoledì e così via con una successione che si svolge con una logica che vedremo più avanti.

Ci sono alcune date nel corso dell’anno che cadono sempre nel doomsday, da queste si può partire per calcolare il giorno di una qualunque data. Per esempio il doomsday del 2015 è sabato e cadranno di sabato i giorni 03 gennaio, 31 gennaio, i giorni divisibili per 7 dei mesi di febbraio e marzo (7, 14, ecc.), mentre per tutti gli altri mesi vige questa semplice regola mnemonica, nei mesi pari: 04/04, 06/06, 08/08 ecc. sono doomsday, cioè nei mesi pari il giorno uguale al numero del mese è sempre doomsday. Nei mesi dispari invece si può usare un altro semplice trucco per memorizzare i doomsday: i giorni sono 05/09 e 09/05 nonché 11/07 e 07/11. Per la loro simmetria basta fissarne a mente due e conoscere automaticamente gli altri due (in effetti in lingua inglese è possibile usare un trucco mnemonico più forte). Quanto detto vale per gli anni non bisestili come appunto il 2015; gli anni bisestili differiscono solo per quanto riguarda i primi due mesi del calendario.
La regola completa consiste nel distinguere, per i primi due mesi dell’anno, degli anni bisestili dai non bisestili:

Anni non bisestili: sono Doomsday

3 e 31 Gennaio
7, 14, 21, 28 Febbraio

Anni bisestili: sono doomsday

3 e 31 Gennaio
1 e 29 Febbraio

Da notare che l’ultimo giorno del mese di Febbraio è sempre doomsday (sia esso il 28 o il 29).
Per tutti gli altri mesi valgono sempre le regole sopra esposte che sintetizziamo di seguito:

a Marzo sono doomsay il 7, 14, 21 e 28
nei mesi dispari sono le seguenti date simmetriche: 9/5, 11/7, 5/9, 7/11
nei mesi pari: i giorni con lo stesso numero del mese: 4/4, 6/6, 8/8, 10/10, 12/12

Inoltre ci sono alcune date facili da ricordare corrispondenti ad alcune ricorrenze; il 4 Luglio (in USA il giorno dell’Indipendenza) e il 25 aprile (in Italia la Festa della Liberazione); ferragosto, cioè il 15 Agosto, il giorno di Halloween (31 Ottobre), San Silvestro 26 dicembre, cioè il giorno dopo Natale. Per i napoletani può essere utile ricordare che il giorno di San Gennaro (19 Settembre) è un doomsday.
Ci sono poi date che hanno un significato personale e facili da ricordare: anche queste possono essere usate come riferimento, per esempio cade in un doomsday la mia data di nascita (ma anche quella di Conway). Nell’arco dell’anno troviamo quindi molti doomsday facili da ricordare. Volendo stabilire il giorno della settimana di una qualunque data basta cercare il doomsday più vicino.
Resta solo da capire come stabilire il Doomsday dell’anno: l’algoritmo non è molto semplice per persone normali, mentre può risultare estremamente facile da memorizzare ed applicare per una persona con il cervello di Conway.

Per semplificare il ragionamento consideriamo questa tabella:

Lun.	Mar.	Mer.	Gio.	Ven.	Sab.	Dom.
1898	1899	1900	1901	1902	1903	→
1904	1905	1906	1907	→	1908	1909
1910	1911	→	1912	1913	1914	1915
→	1916	1917	1918	1919	→	1920
1921	1922	1923	→	1924	1925	1926
1927	→	1928	1929	1930	1931	→
1932	1933	1934	1935	→	1936	1937
1938	1939	→	1940	1941	1942	1943
→	1944	1945	1946	1947	→	1948
1949	1950	1951	→	1952	1953	1954
1955	→	1956	1957	1958	1959	→
1960	1961	1962	1963	→	1964	1965
1966	1967	→	1968	1969	1970	1971
→	1972	1973	1974	1975	→	1976
1977	1978	1979	→	1980	1981	1982
1983	→	1984	1985	1986	1987	→
1988	1989	1990	1991	→	1992	1993
1994	1995	→	1996	1997	1998	1999
→	2000	2001	2002	2003	→	2004
2005	2006	2007	→	2008	2009	2010
2011	→	2012	2013	2014	2015	→
2016	2017	2018	2019	→	2020	2021
2022	2023	→	2024	2025	2026	2027
→	2028	2029	2030	2031	→	2032
2033	2034	2035	→	2036	2037	2038
2039	→	2040	2041	2042	2043	→
2044	2045	2046	2047	→	2048	2049
2050	2051	→	2052	2053	2054	2055
→	2056	2057	2058	2059	→	2060
2061	2062	2063	→	2064	2065	2066
2067	→	2068	2069	2070	2071	→
2072	2073	2074	2075	→	2076	2077
2078	2079	→	2080	2081	2082	2083
→	2084	2085	2086	2087	→	2088
2089	2090	2091	→	2092	2093	2094
2095	→	2096	2097	2098	2099	2100

E la sequenza sembra abbastanza chiara: il doomsday si sposta di un giorno ogni anno, nei bisestili si sposta di due. Il ciclo si ripete in 28 anni.

Il gioco che faceva spesso Conway per stupire l’interlocutore era indovinare il giorno della settimana ad esempio quello della sua data di nascita; ad esempio se l’interlocutore fosse nato il 26 agosto 1965, nota dalla tabella che il doomsday del 1965 è la domenica (Conway era in grado di determinarlo con calcoli basati sull’aritmetica modulare a mente). La data di agosto di riferimento è l’otto agosto (08/08), che è capitata quindi di domenica, con un semplice conteggio si può capire che il 26 agosto 1965 era giovedì.

[1] John H. Conway; R. T. Curtis; S. P. Norton; R. A. Parker; R. A. Wilson: “Atlas of Finite Groups: Maximal Subgroups and Ordinary Characters for Simple Groups” Oxford, 1985
[2] Marcus Du Sautoy: “Il disordine perfetto: L’avventura di un matematico nei segreti della simmetria” BUR, 2010

	Blu	Verde	Rosso	Giallo
Do
Do#/Reb
Re
Re#/Mib
Mi
Fa
Fa#/Solb
Sol
Sol#/Lab
La
La#/Sib
Si
Do