I moderni strumenti musicali producono una serie di note codificate in base a criteri che hanno avuto una interessante evoluzione nel corso dei secoli.
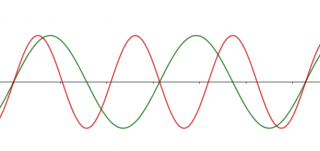
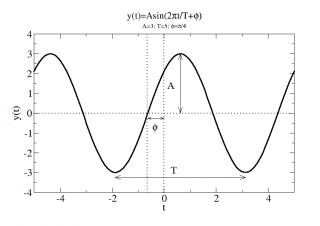
Oggi sappiamo il suono è un’onda trasmessa in un mezzo, caratterizzata quindi da intensità, lunghezza d’onda e frequenza nonché dalla propria forma d’onda. L’immagine che segue rappresenta un’onda sinusoidale, che si può descrivere cioè tramite la funzione trigonometrica seno. Ma la forma dell’onda può anche essere diversa, ad esempio quadra o triangolare. Il suono prodotto avrà una differente connotazione.
La caratteristica dell’onda che ci interessa in questo caso è la frequenza, ovvero il numero di oscillazioni che l’onda effettua in un secondo (1 Hz =1 ciclo/s). Ad onde con differente frequenza corrispondono differenti percezioni uditive. Le note più gravi hanno una frequenza bassa, quanto tanto più sono acute tanto più la frequenza sarà alta. La corrispondenza tra nota e frequenza è stata codificata per la prima volta da Pitagora nel VI secolo a.C. in maniera analoga a quanto esposto di seguito.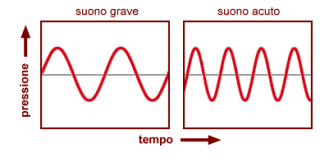 
Una corda posta in tensione e fatta vibrare produce un suono. Egli studiò il modo con cui i suoni variano a mano a mano che si riduce la lunghezza della corda: la frequenza con cui la corda vibra aumenta quando la corda viene accorciata e i suoni ottenuti risultano più acuti. Si può notare che il suono prodotto da una corda completamente estesa confrontato con il suono dalla stessa corda ridotta alla metà risulta sovrapponibile benché diverso. Ciò è dovuto al fatto che dimezzando la lunghezza della corda la sua frequenza si raddoppia: le due onde sonore hanno forme strettamente correlate.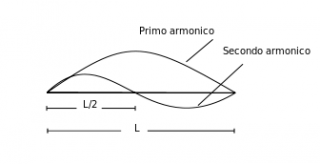
In questo caso si dice che i suoni prodotti dalle due corde hanno la distanza di una ottava. Nella notazione moderna le note che distano un’ottava hanno lo stesso nome, infatti entrambe le note di seguito rappresentate sono chiamate Do.
OttavaRaddoppiando o dimezzando la frequenza di una nota si produce la stessa nota trasposta di un’ottava. |
Due suoni prodotti in sequenza possono dare un effetto “gradevole” o “sgradevole” all’orecchio umano.
Tra i vari abbinamenti possibili Pitagora notò che riducendo la corda ad \frac{1}{3} o, il che è lo stesso, ai \frac{2}{3} (suonando cioè la nota un ottavo superiore), la nota prodotta risulta “gradevolmente abbinata” alla prima nota.
Il rapporto tra le frequenze di queste due note è 3:2, l’inverso del rapporto tra le lunghezze delle corde.
Ciò rende ragione della sensazione di “giusto abbinamento”: ogni due oscillazioni della prima corda la seconda oscilla 3 volte.
La nota separata dalla prima da un rapporto tra le frequenze di \frac{3}{2} viene detta quinta giusta.
QuintaMoltiplicando per \frac{3}{2} (o per \frac{2}{3}) la frequenza di una nota si produce una nota che “si abbina bene” con la prima. |
Mediante un procedimento matematico si individuano i rapporti che corrispondono a nuove frequenze. Proseguendo di quinta in quinta si ottiene una sequenza di note che “suonano bene insieme”. La prima nota è in rapporto 1:1 con se stessa, la seconda è 3:2 della prima. Individuiamo una nuova nota in modo che abbia un rapporto 3:2 con quest’ultima; poiché \frac{3}{2} × \frac{3}{2} = \frac{9}{4}, essa è in rapporto 9:4 con la prima.
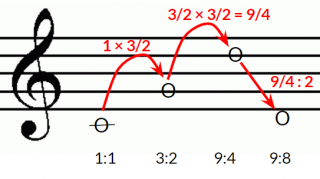Poiché \frac{9}{4} > 2 questa nota ha superato l’ottava della nota base; riportiamola quindi nell’ambito della prima ottava dividendo la frazione per 2:
\frac{9}{4} × \frac{1}{2} = \frac{9}{8}.
Otteniamo quindi un suono con un rapporto di frequenza 9:8 rispetto alla nota di riferimento.
Cerchiamo adesso la quinta del suono 9:8 moltiplicando questo rapporto per \frac{3}{2} e otteniamo 27:16.
La successiva è \frac{27}{16} × \frac{3}{2} =81:32. Anche quest’ultima frazione rappresenta una nota esterna all’ottava, per cui va divisa per 2, ottenendo 81:64. L’ultimo rapporto sarà \frac{81}{64} × \frac{3}{2} = 243:128.
Aggiungiamo infine il suono la cui quinta è 1:1, invertiamo cioè il calcolo ottenendo la nota 2:3, infatti la quinta di 2:3 è \frac{2}{3} × \frac{3}{2} = 1.
Questa nota va riportata anch’essa nella giusta ottava moltiplicandola 2 e ottenendo infine 4:3.
Questo procedimento ha generato la sequenza di rapporti:
1:1, 3:2, 9:8, 27:16, 81:64, 243:128, 4:3
che ordinanti in senso crescente diventano
1:1, 9:8, 81:64, 4:3, 3:2, 27:16, 243:128
A queste note associamo convenzionalmente dei nomi, che per tradizione sono nell’ordine Do, Re, Mi, Fa, Sol, La, Si.
Il rapporto tra due note successive è \frac{9}{8} tranne che tra Fa e Mi e tra Si e Do per i quali è \frac{256}{243}. Il primo intervallo è detto tono, mentre il secondo è il semitono.
La scala musicale così ottenuta può essere ampliata aggiungendo un suono tra le note separate da un tono.
Ad esempio dal Do si può passare al Do♯ aggiungendo un semitono ovvero \frac{256}{243}. Il Do♯ sarà rappresentato quindi dalla frazione 1 × \frac{256}{243} = \frac{256}{243}.
A sua volta il Re♯ si otterrà da \frac{9}{8} × \frac{256}{243} = \frac{2304}{1944} = \frac{32}{27}. In conclusione:
Do♯ = 1 × \frac{256}{243} = \frac{256}{243}
Re♯ = \frac{9}{8} × \frac{256}{243} = \frac{32}{27}
Fa♯ = \frac{4}{3} × \frac{256}{243} = \frac{1024}{729}
Sol♯ = \frac{3}{2} × \frac{256}{243} = \frac{128}{81}
La♯ = \frac{27}{16} × \frac{256}{243} = \frac{16}{9}.
Si può notare che spostarsi di due semitoni non equivale a spostarsi di un tono, infatti se dal Re ci si sposta di un semitono all’indietro si ottiene (\frac{9}{8})/(\frac{256}{243})=\frac{2187}{2048}.
Questa nota, diversa dal Do♯, è detta Re♭.
Tra il Do♯ e il Re♭ vi è una distanza di (\frac{2187}{2048})/(\frac{256}{243})= \frac{531441}{524288} ≅ 1,0136.
Tale intervallo è il cosiddetto comma pitagorico, che seppure sia piccolo è apprezzabile dall’orecchio umano.
Le seguenti note completano la scala cromatica:
Re♭ = (\frac{9}{8})/(\frac{256}{243}) = \frac{2187}{2048}
Mi♭ = (\frac{81}{64})/(\frac{256}{243}) = \frac{19683}{16384}
Sol♭ = (\frac{3}{2})/(\frac{256}{243}) = \frac{729}{512}
La♭ = (\frac{27}{16})/(\frac{256}{243}) = \frac{6561}{4096}
Si♭ = (\frac{243}{128})/(\frac{256}{243}) = \frac{59049}{32768}
Questa è la rappresentazione delle note sul pentagramma: il numero di note della scala pitagorica cromatica è 17.
In passato sono stati costruiti strumenti che rispettano la scala pitagorica. Per noi hanno un aspetto poco usuale.
esposto al Museo del Castello di Gesualdo
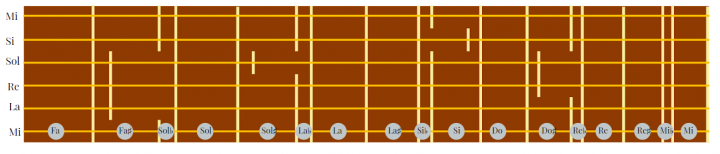
In questo ipotetico manico di chitarra sono rappresentate le posizioni corrispondenti alla scala cromatica pitagorica
Per evitare questi e altri inconvenienti nei secoli si sono ideate altre scale, fino ad arrivare al temperamento equabile:
- è stato annullato il comma pitagorico: Do♯ e il Re♭ coincidono
- tra due semitoni vi è un rapporto costante, i suoni ottenuti sono prossimi ai suoni della scala pitagorica
- le note della scala cromatica sono ridotte a 12
Poiché si richiede che tra due semitoni il rapporto sia costante e che le note distanti un’ottava abbiano un rapporto pari a 2, il rapporto costante tra i semitoni deve essere un numero k tale che
k12 = 2 cioè k=12√2 ≈ 1,05946.
Posto k=12√2 ≈ 1,05946, si può notare che questa quantità è molto prossima al rapporto \frac{256}{243} ≈ 1,0535 che contraddistingue la distanza tra Si e Do e tra Mi e Fa nella scala pitagorica.
Inoltre k2 ≈ 1,12246 risulta una buona approssimazione del rapporto \frac{9}{8} = 1,125 cioè l’ampiezza di un tono.
Noto già nell’antichità (Aristosseno di Taranto intorno al 320 a.C.), questo tipo di temperamento ha impiegato secoli prima di essere accettato, anche per la presenza del fattore irrazionale 12√2.
L’aspetto della tradizionale tastiera del pianoforte è data dalla scala così costruita
| Do | Re | Mi | Fa | Sol | La | Si | Do1 | |||||
| 1 | 12√2 | (12√2)2 | (12√2)3 | (12√2)4 | (12√2)5 | (12√2)6 | (12√2)7 | (12√2)8 | (12√2)9 | (12√2)10 | (12√2)11 | (12√2)12 |
La tastiera della chitarra tradizionale confrontata con un’ipotetica chitarra in scala pitagorica rende maggiormente l’idea di cosa si intenda per temperamento equabile. Le posizioni sulla prima sono una buona approssimazione dei corrispondenti sulla seconda, e così anche i suoni che si ottengono.