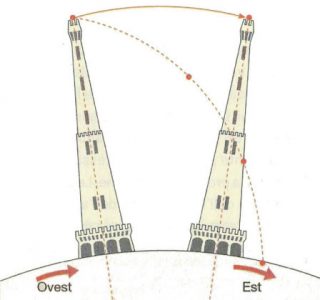
Viene qui illustrato il celebre esperimento di Guglielmini eseguito a Bologna nel 1790 mediante precise misurazioni dello scostamento dalla verticale di biglie di piombo lasciate cadere dalla Torre degli Asinelli.
Il risultato di questo esperimento permise di mettere in evidenza per la prima volta il moto di rotazione della Terra, prima cioè dell’esperimento del pendolo di Foucault nel 1851, infatti se la Terra fosse completamente immobile gli oggetti cadrebbero lungo una perfetta verticale.
In sintesi la base della torre e la sua estremità si muovono a velocità leggermente diverse: mentre la Terra ruota di un certo angolo, il vertice percorre un tratto maggiore rispetto a quello percorso dalla base quindi il vertice si muove più velocemente. Un oggetto che cade dalla torre avrà quindi una velocità orizzontale maggiore rispetto al suolo. Durante la caduta quindi percorre uno spazio maggiore rispetto al punto sulla sua verticale, cadendo quindi leggermente più ad est.
In dettaglio la Terra, in moto attorno al proprio asse, ruota ad una velocità v_0:
v_0 = \frac{C_0}{T} = \frac{2 \pi r_0 }{T} = \frac{2 \pi R_T }{T} \cos \alphadove C_0 e R_T indicano rispettivamente la circonferenza e il raggio terrestre, mentre T è il periodo di rotazione terrestre. Un oggetto posto ad un’altezza h, compie una circonferenza C_h e pur avendo la stessa velocità angolare, sarà caratterizzato da una velocità v_h \gt v_0 :
v_h = \frac{C_h}{T} = \frac{2 \pi r_h }{T} = \frac{2 \pi (R_T+h) }{T} \cos \alphaLa differenza tra le due velocità sarà:
\Delta v = v_h - v_0 = \frac{2 \pi h }{T} \cos \alpha
Calcolo il tempo di caduta imponendo nell’equazione y_f=y_0 - \frac{1}{2} g t^2
le condizioni y_0=h e y_f=0:
In questo intervallo di tempo la biglia avrà compiuto uno spostamento “orizzontale” maggiore del suolo terrestre:
\Delta s = \Delta v t = \frac{2 \pi h }{T} \cos \alpha \frac{2 \pi h }{T} \cos \alpha \sqrt[]{\frac{2h}{g}} = \left( \frac{2 \pi}{T} \frac{2}{g} \right) \sqrt[]{h^3} \cos \alpha
Dal momento che T=24 h = 86400 s e g=9,81 m/s^2 si può porre: k=\frac{2 \pi}{T} \frac{2}{g} \approx 3,28 \times 10^{-5}
Pertanto:
\Delta s = k \sqrt[]{h^3} \cos \alpha , da cui deduciamo che:
* all’equatore la deviazione è massima;
* ai poli non si ha deviazione;
* alle latitudini intermedie aumenta con la potenza di 3/2 rispetto all’altezza.
Intorno alla latitudine di 45° si ha (Bologna è a 44°30′): \cos \alpha = \frac{\sqrt[]{2}}{2}.
Quindi per un dislivello di h=100 m era atteso uno scostamento dalla verticale di circa: \Delta s = k \sqrt[]{100^3} \frac{\sqrt[]{2}}{2} \approx 0,023 m
Le misure effettuate si avvicinarono molto a questo valore, infatti all’epoca fu misurato uno scostamento di 1,7 cm.