caduta – L'Entropia nell'Universo può solo aumentare

Il problema della catenaria

12/18/201307/27/2020 franzpizzo

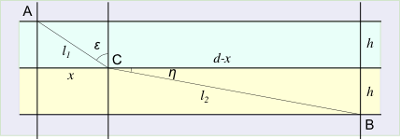
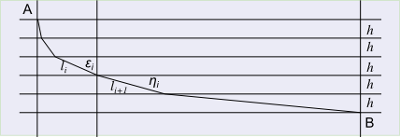
Un cavo vincolato ai suoi estremi a due punti fissi e soggetto alla sola forza peso assume una configurazione caratteristica simile ad una parabola; tale curva viene detta catenaria.

Descrizione del problema della catenaria

La curva “assomiglia” ad una parabola in quanto ha nella sua estremità inferiore un vertice, è concava verso l’alto e simmetrica rispetto ad un asse passante per il vertice.
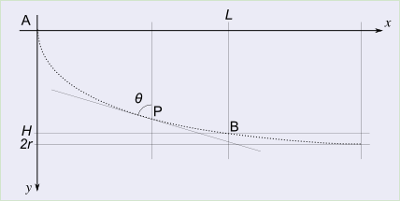
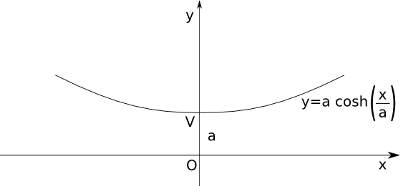
Consideriamo un sistema di riferimento in cui l’asse delle ordinate coincide con l’asse di simmetria, orientato nel verso della concavità.
A partire dal vertice muoviamoci lungo la curva percorrendo uno dei suoi rami, per esempio quello di ascissa positiva, per un tratto di lunghezza

s

fino al punto

P

.
Le coordinate del punto

P

dipendono dal tratto

s

percorso:

\begin{cases} x = x(s) \\ y = y(s) \end{cases}

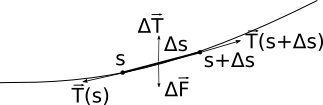
Affinché sussista l’equilibrio statico la risultante delle forze che agiscono su un qualunque tratto $\Delta\,s$ del cavo è nulla. Su $\Delta\,s$ agisce una forza peso che dipende dalla densità lineare $\lambda$ del cavo, di modulo $\Delta\,F = \lambda\;g\;\Delta\,s$ , diretta verso il basso.
Gli estremi di $\Delta\,s$ sono invece soggetti alle tensioni $\vec {T}(s)$ e $\vec {T}(s + \Delta\,s)$ la cui risultante è $\Delta\,\vec{T} = \vec{T} (s + \Delta\,s) - \vec{T}(s)$ . Per la staticità della configurazione la risultante delle forze a cui è soggetto il segmento $\Delta\,s$ è nulla, quindi $\Delta\,\vec{T}= \lambda\;h\;\Delta\,s\;\hat j$ , dove $\hat j$ è il versore dell’asse delle ordinate.

Bilancio delle forze agenti su un tratto di corda

Passando alle componenti

\begin{cases} \Delta\,T_x = 0 \\ \Delta\,T_y = \lambda\;g\;\Delta\,s\end{cases}

Poiché queste uguaglianze valgono anche per un tratto di curva infinitesimo $ds$ abbiamo

\begin{cases}d T_x = 0\\ d T_y = \lambda\;g\;d s\end{cases} \Rightarrow \\{ \begin{cases} & \int_{T_x (0)}^{T_x (s)} d \tau = c\\ & \int_{T_y (0)}^{T_y (s)} d \tau = \int_{0}^{s} g \lambda d \sigma\end{cases} \Rightarrow \\ \begin{cases} T_x (s) - T_x (0) = c\\ T_y (s) - T_y (0) = g\;\lambda\;s \end{cases} }

Quindi $T_x (s) = T_x (0) + c$ e dal momento che $T_x (0) = T_x (0) + c$ allora $c = 0$ , cioè la componente orizzontale della tensione è costante su tutto il ramo della corda di ascissa positiva, ponendo perciò $T_0 = T_x (0)$ , avremo $T_x (s) = T_0$ lungo tutta la corda.
D’altra parte $T_y$ , la componente verticale della tensione, è dovuta al peso del cavo di lunghezza $s$ compreso tra il vertice e il punto $P$ , quindi si ha $T_y(0) = 0$ . Abbiamo infine

\begin{cases} T_x = T_0\\ T_y = g\;\lambda\;s \end{cases}

che può essere scritta come

\begin{cases} T \frac{dx}{ds} = T_0\\ T \frac{dy}{ds} = g\;\lambda\;s \end{cases}

avendo considerato le componenti $\frac{dx}{ds}$ e $\frac{dy}{ds}$ del versore della tangente alla curva e $T$ il modulo della tensione $\vec{T}$ .

Dalle due equazioni otteniamo

$T \frac{dy}{ds} \frac{1}{T} \frac{dx}{ds} = \frac{g \lambda}{T_0} \Rightarrow \frac{dy}{dx}=\frac{g \lambda}{T_0} s$ e ponendo $a=\frac{T_0}{g \lambda} \Rightarrow \frac{dy}{dx}=\frac{s}{a}$ .

Inoltre poiché

(ds)^2 = (dx)^2 + (dy)^2 \Rightarrow \\ ds = \sqrt{1 + \left ( \frac{dy}{dx} \right )^2 } dx \Rightarrow \\ ds = \sqrt{1 + \left ( \frac{s}{a} \right )^2 } dx \Rightarrow

\Rightarrow dx = \frac{ds}{\sqrt{1 + \left ( \frac{s}{a} \right )^2 } }\Rightarrow \\ dx = a \frac {d \left ( \frac{s}{a} \right )}{\sqrt{1 + \left ( \frac{s}{a} \right )^2 }}

integrando

\int_{0}{x} d \xi = a \int_{0}{\frac{a}{s}} \frac{dt}{\sqrt{1 + t^2}} \Rightarrow \\ x=a \left [ log( t + \sqrt{1 + t^2} ) \right ]_0^\frac{s}{a} \Rightarrow

\Rightarrow x = a\;log \left ( \frac{s}{a} + \sqrt{1 + \left ( \frac{s}{a}\right )^2} ) \right ) \Rightarrow \\ \frac{x}{a}= log \left ( \frac{s}{a} + \sqrt{1 + \left ( \frac{s}{a}\right )^2} ) \right )

Quest’ultima relazione può essere invertita scrivendo $s$ in funzione di $x$ :

e^{ \frac{x}{a} } = \frac{s}{a} + \sqrt{1+ \left ( {\frac{s}{a}} \right )^2} \Rightarrow e^{2 \frac{x}{a} } - 2\; \frac{s}{a}\; e^{ \frac{x}{a} } + \left ( {\frac{s}{a}} \right )^2 = 1 + \left ( {\frac{s}{a}} \right )^2 \Rightarrow

$\Rightarrow e^{\frac{x}{a} } - 1 = 2\;{\frac{s}{a}}\; e^{\frac{x}{a} } \Rightarrow \\ 2\;{\frac{s}{a}} = e^{\frac{x}{a} } - e^{- {\frac{x}{a}} } \Rightarrow \\s = a\; \frac{{e^{\frac{x}{a} } - e^{-\frac{x}{a}} }}{2}$

Cioè

s = a\;\sinh \left ( \frac{x}{a} \right )

Quindi $\frac{dy}{dx} = \frac{s}{a} \Rightarrow \frac{dy}{dx} = \sinh \left ( \frac{x}{a} \right ) \Rightarrow y = a\;\cosh \left ( \frac{x}{a} \right ) + c$ dove $c$ si può scegliere liberamente traslando in maniera opportuna il sistema di coordinate. Imponendo $y(0)=a$ si ha $c=0$ e pertanto $y = a\;\cosh \left ( \frac{x}{a} \right )$ .
Diverso è il caso di un cavo soggetto al un carico uniforme $p$ e per il quale il carico dovuto al proprio peso è trascurabile. Ciò si verifica nei classici ponti sospesi, in cui il cavo funge da struttura portante.

La forza verticale che agisce su ogni tratto

\Delta\,s

è in questo caso

\Delta\,\vec{F}= p\;\Delta\,x\;\hat j

per cui possiamo riscrivere le equazioni della tensione in questo modo

\begin{cases} \Delta\,T_x = 0 \\ \Delta\,T_y = p\; \Delta\,x \end{cases} \Rightarrow \\ \begin{cases} d T_x = 0 \\ & d T_y = p\; d x \end{cases} \Rightarrow \\ \begin{cases} T_x = T_0 \\ T_y = p\; x \end{cases} \Rightarrow \\ \begin{cases} T \frac{dx}{ds} = T_0 \\ T \frac{dy}{ds} = p\; x \end{cases} \Rightarrow \frac{dy}{dx} = \frac{p}{T_0}\; x

da cui
$y = \frac{p}{2\;T_0}\;x^2 + c$ .

Scegliendo opportunamente il sistema di riferimento in modo che $y(0)=0$ si ha $c=0$ e quindi $y = \frac{p}{2\;T_0}\;x^2$ che si riconosce essere l’equazione della parabola.

La brachistocrona

03/16/201307/27/2020 franzpizzo

Il problema della brachistocrona consiste nel trovare la particolare traiettoria che un corpo, soggetto alla sola forza peso, deve compiere nel passare da un punto $A$ ad un punto $B$ posto ad una quota più bassa, che sia tale da minimizzare il tempo di percorrenza.

La ricerca di questa curva può avvenire notando l’analogia con quanto avviene per la rifrazione della luce. Nel passaggio da un mezzo all’altro la luce varia la sua velocità e il percorso che compie nell’unire due punti è quello che gli permette di impiegare meno tempo. I punti $A$ e $B$ si trovano agli estremi di due strati di materiali diversi e di uguale spessore h. La luce attraverserà la linea di separazione in un punto $C$ da determinare. Nei due strati la luce ha velocità rispettivamente

$v_1$ e $v_2$ e percorre i tratti $l_1=\sqrt{h^2 + x^2}$ e $l_2=\sqrt{h^2 + (d-x)^2}$ con tempi di percorrenza
$t_1 = \frac{l_1}{v_1} = \frac{\sqrt{h^2 + x^2}}{v_1}$ e $t_2=\frac{l_2}{v_2}=\frac{\sqrt{h^2 + (d-x)^2}}{v_2}$ .
Il tempo totale di percorrenza risulta quindi
$t = t_1 + t_2 = \frac{\sqrt{h^2 + x^2}}{v_1} + \frac{\sqrt{h^2 + (d-x)^2}}{v_2}$ .
Scegliamo la posizione del punto $C$ in modo da minimizzare il tempo di percorrenza. Il punto di minimo dell’espressione del tempo deve avere necessariamente derivata nulla:

$\frac{dt}{dx} = \frac{1}{2} \frac{1}{v_1} \frac{2 x}{\sqrt{h^2 + x^2}} + \frac{1}{2} \frac{1}{v_2} \frac{-2 (d-x) }{\sqrt{h^2 + (d-x)^2}}=$
$= \frac{x}{v_1 \sqrt{h^2 + x^2}}-\frac{d-x}{v_2 \sqrt{h^2 + (d-x)^2}} = \frac{x}{l_1}-\frac{d-x }{v_2 l_2} = \frac{\sin \varepsilon }{v_1}-\frac{\sin \eta }{v_2} = 0$

Dove con $\varepsilon$ e $\eta$ abbiamo indicato gli angoli di incidenza e di rifrazione dispetto alla normale alla superficie di separazione. Il punto $C$ è determinato dalla soluzione della precedente equazione, inoltre si ha
$\frac{\sin \varepsilon }{v_1} = \frac{\sin \eta }{v_2} = \frac{1}{k}$
con $k$ una opportuna costante.

Si può generalizzare questo risultato applicando più volte ad una successione di strati contigui di uguale spessore e di materiali diversi. Nello strati i-esimo la luce percorre il tratto $l_i$
ad una velocità $v_i$ e resta determinato il punto di passaggio $x_i$ tra ciascuno strato. Il tempo totale impiegato per passare dal punto $A$ al punto $B$ è dato da:

$t=t_1+t_2+\ldots+t_n=\frac{l_1}{v_1}+\frac{l_2}{v_2}+\ldots+\frac{l_n}{v_n}$ .

Quando l’ampiezza degli strati tende a zero e il loro numero tende all’infinito, la successione di tratti rettilinei tende ad una curva. Poiché

$\sin \varepsilon_i = v_i \frac{\sin \eta_i}{v_{i+1}}$ allora $\sin \varepsilon_i$ sarà tanto piccolo quanto più $v_i$ è piccolo e quindi se la velocità nel primo tratto tende a zero allora $\varepsilon_i$ tende a zero, cioè la direzione iniziale tende alla verticale. Allo stesso modo, dal momento che $\sin \eta_{i+1} = v_{i+1} \frac{\sin \varepsilon_i}{v_i}$ allora $\sin \eta_{i+1}$ crescerà al crescere di $v_{i+1}$ e poiché il massimo della funzione seno si ha per $\frac{\pi}{2}$ , la velocità massima si raggiunge quando il moto è orizzontale.

Applichiamo questo risultato al caso di un corpo che transita dal punto $A$ al punto $B$ e cerchiamo la traiettoria che ottimizzi il tempo di percorrenza.
Consideriamo un sistema di riferimento con origine coincidente con il punto $A$ e l’asse delle ordinate orientato verso il basso: $A(0,0)$ e $B(L,H)$ .

L’energia totale di un corpo soggetto alla forza peso è
$E= \frac{1}{2} m v^2 + m g y$ .

Tale quantità è costante dal momento che non agiscono forze non conservative inoltre imponendo la condizione iniziale $v_A=0$

E_A=0 \Rightarrow \frac{1}{2} m v^2 + m g y = 0

e quindi $v^2 = 2 g y$ .

Sia $\theta$ l’angolo che la tangente alla traiettoria forma con la verticale, poiché

$\frac{\sin \theta}{v} = \frac{1}{k}$ costante allora

v^2 \sin^2 \theta = k^2 \Rightarrow \frac{2 g y}{\sin^2 \theta} = k^2

abbiamo $y= \frac{k^2}{2 g} \sin^2 \theta$ .

L’angolo $\theta$ tende a $\frac{\pi}{2}$ .

Indichiamo invece con $2 r$ l’ordinata relativa alla massima velocità; avremo $2 r = \frac{k^2}{2 g} \sin \frac{\pi}{2} = \frac{k^2}{2 g}$
e quindi $k^2 = 4 g r$ .

Sostituiamo il valore di $k^2$ nell’espressione dell’ordinata: $y=\frac{4 g r}{2 g} \sin^2 \theta = 2 r \sin^2 \theta$ .
Derivando quest’ultima espressione rispetto a $\theta$ :

$\frac{dy}{d\theta}=2 r \cdot 2 \sin \theta \cos \theta = 2 r \sin 2 \theta$ .

Poiché

$\frac{dx}{dy}=\tan \theta \Rightarrow \frac{dx}{d\theta}=\frac{dx}{dy}\frac{dy}{d\theta} = \tan \theta \cdot 4 r \sin \theta \cos \theta =$
$=\frac{\sin \theta}{\cos \theta} \cdot 4 r \sin \theta \cos \theta = 4 r \sin^2 \theta = 2 r (1-\cos 2 \theta)$

Quindi

\begin{cases}\frac{dx}{d\theta} = 2 r ( 1-\cos 2\theta ) \\ \frac{dy}{d\theta} = 2 r \sin 2\theta\end{cases}\Rightarrow\begin{cases}x = r ( 2 \theta-\sin 2\theta ) + c_1 \\ y = -r \cos 2 \theta + c_2\end{cases}

dove $c_1$ e $c_2$ sono determinate a partire dalle condizioni iniziali. È stato supposto che il corpo sia inizialmente fermo in $A$ e quindi il suo moto inizia nella direzione verticale: $\theta_A = 0$

$\begin{cases}0 = r ( 0-\sin 0 ) + c_1\\ 0 = -r \cos 0 + c_2 \end{cases} \Rightarrow \begin{cases} c_1 = 0\\ c_2 = r \end{cases}$ .

La curva cercata si esprime in forma parametrica come

\begin{cases} x = r ( 2 \theta-\sin 2\theta ) \\ y = r ( 1-\cos 2 \theta ) \end{cases}

Si riconosce che tale curva rappresenta una cicloide ossia la curva descritta da un punto su una circonferenza di raggio $r$ quando questi viene fatto rotolare.

Deriviamo queste ultime espressioni rispetto al tempo:

\begin{cases} \frac{dx}{dt} = \frac{dx}{d\theta} \frac{d\theta}{dt} = r ( 2 \theta-\sin 2\theta ) \dot \theta\\ \frac{dy}{dt} = \frac{dy}{d\theta} \frac{d\theta}{dt} = 2 r ( \sin 2\theta ) \dot \theta \end{cases}

Possiamo ricavare l’espressione della velocità del corpo rispetto al parametro $\theta$ .

$v^2 = \left( \frac{dx}{dt} \right)^2 + \left( \frac{dy}{dt} \right)^2 = 4 r \left [ ( 1-\cos 2 \theta )^2 + (\sin 2 \theta)^2 \right] \dot \theta^2 =$
$= 4 r ( 1-2 \cos 2 \theta + \cos^2 2 \theta + \sin^2 2 \theta ) \dot \theta^2 =$
$= 8 r^2 ( 1-\cos 2 \theta ) \dot \theta^2 = 16 r^2 ( \sin^2 \theta ) \dot \theta^2$

Invertiamo tale relazione ricavando $\dot \theta$ :

\dot \theta^2 = \frac {v^2}{16 r^2 \sin^2 \theta} = \frac{k}{16 r^2} = \frac{4 g r }{16 r^2} = \frac{g}{4 r}<br /> \Rightarrow \dot \theta = \frac{1}{2} \sqrt{\frac{g}{r}}

e integrando, e tenendo conto delle condizioni iniziali $\theta_A = 0$ :

\theta = \int \frac{1}{2} \sqrt{\frac{g}{r}} \, dt = \frac{1}{2} \sqrt{\frac{g}{r}} t

Il tempo totale $T$ impiegato per raggiungere il punto più basso, cioè quando
$\theta = \frac{\pi}{2}$ ,
è dato dalla soluzione dall’equazione
$\frac{\pi}{2} = \frac{1}{2} \sqrt{\frac{g}{r}} T \Rightarrow T = \pi \sqrt{\frac{r}{g}}$

Poiché l’espressione parametrica della curva si può scrivere come

\begin{cases} x = r ( \sqrt{\frac{g}{r}} t-\sin \sqrt{\frac{g}{r}} t ) \\ y = r ( 1-\cos \sqrt{\frac{g}{r}} t )\end{cases}

Al tempo $T = \pi \sqrt{\frac{r}{g}}$ il corpo si troverà nel punto

$\begin{cases} x = r ( \pi-\sin \pi ) \\ y = r ( 1-\cos \pi ) \end{cases} \Rightarrow \begin{cases} x = \pi r \\ y = 2 r \end{cases}$ .

Moto di un proiettile

08/14/201207/27/2020 franzpizzo

Studiamo il moto di un oggetto a cui viene impressa una velocità iniziale $\vec{v} = \left( v_{0x}, v_{0y} \right)$

e soggetto alla forza di gravitazionale della Terra.
Scegliamo un sistema di riferimento con l’origine coincidente con la posizione iniziale del corpo e l’asse delle ordinate parallelo alla direzione della forza ma con verso opposto. Si riconosce che il moto di quest’oggetto può essere visto come composizione di un moto rettilineo lungo l’asse delle ascisse e un moto uniformemente accelerato lungo l’asse delle ordinate.
Le equazioni del moto espresse in questo sistema di riferimento sono

\begin{cases}x=v_{0x} t \\y=v_{0y} t -\frac{1}{2}g t^2\end{cases}

Dove le componenti della velocità si possono esprimere come

\begin{cases}v_{0x}=v_0 \cos \alpha \\v_{0y}=v_0 \sin \alpha\end{cases}

Pertanto

\begin{cases}v_{0x}=v_0 \cos \alpha \\v_{0y}=v_0 \sin \alpha\end{cases}\Rightarrow {y=\tan \alpha x -\frac{1}{2} \frac{g}{\cos \alpha} x^2}

Quest’ultima è l’equazione della traiettoria, che si riconosce essere una parabola.

Riguardo il moto di quest’oggetto possiamo ricavare i seguenti parametri.

Il tempo di volo

Poniamo $y=0 \Rightarrow {v_{0y} t -\frac{1}{2} g t^2 = 0 \Rightarrow {t=0\;\; e\;\; t=2 \frac{v_{0y}}{g}= 2 \frac{v_0}{g} \sin \alpha }}$ .

Gittata

Basta ricavare la distanza raggiunta dal termine del tempo di violo

x=v_{0x}\; 2 \frac{v_{0y}}{g}= 2 \frac{v_{0x} v_{0y}}{g}= 2 \frac{v_{0}^2}{g} \sin \alpha \cos \alpha = \frac{v_{0}^2}{g} \sin 2 \alpha

Vertice della parabola

Si può calcolare immediatamente come metà della gittata oppure trovando l’istante in cui componente verticale della velocità si annulla e quindi
$v=v_{0y}-gt \Rightarrow 0=v_{0y}-gt \Rightarrow t=\frac{v_{0y}}{g}$ e sostituendo nell’equazione oraria del moto nella direzione orizzontale si ottiene
$x =v_{0x}t=v_{0x}\frac{v_{0y}}{g} =\frac{v_{0x} v_{0y}}{g} =\frac{v_{0}^2}{g} \sin \alpha \cos \alpha = \frac{1}{2}\frac{v_{0}^2}{g} \sin 2 \alpha$ .
Analogamente si ottiene l’altezza massima
$y =\frac{v_{0y}}{v_{0x}}\frac{v_{0x} v_{0y}}{g}-\frac{1}{2}\frac{g}{v_{0x}^2}\frac{v_{0x}^2 v_{0y}^2}{g}^2 =\frac{v_{0y}^2}{g}-\frac{1}{2}\frac{v_{0y}^2}{g} =\frac{1}{2}\frac{v_{0y}^2}{g} =\frac{1}{2}\frac{v_0^2}{g}\sin^2 \alpha$ .

Fissata la gittata $\ell$ ricaviamo:

$\ell=2 \frac{v_{0x} v_{0y}}{g} \Rightarrow { \ell=2 \frac{v_{0}^2}{g} \sin 2 \alpha \Rightarrow { v_{0}^2=\frac{\ell g}{\sin 2 \alpha} \Rightarrow { v_{0}=\sqrt{\frac{\ell g}{\sin 2 \alpha}} }}}$ .

Da quest’ultima si ricava che deve necessariamente essere $0<\alpha<\frac{\pi}{2}$ .
La velocità da imprimere alla partenza dipende quindi solo dall’angolo $\alpha$ . Derivando l’espressione della
velocità rispetto all’angolo otteniamo

$2 \sqrt{\ell g}\left(-\frac{1}{2}\right) \sin^{-{3}{2}} 2 \alpha \cos 2 \alpha = -\sqrt{\ell g}\frac{\cos 2 \alpha}{\sqrt{\sin^3 2 \alpha}}$ .

Imponiamo

$-\sqrt{\ell g}\frac{\cos 2 \alpha}{\sqrt{\sin^3 2 \alpha}}=0 \Rightarrow 2 \alpha = \frac{\pi}{2} \Rightarrow \alpha = \frac{\pi}{4}$ .

Questo valore rappresenta l’angolo per il quale $v_0$ è minima e $v_0=\sqrt{\ell g}$ è la velocità minima da imprimere all’oggetto per raggiungere $\ell$ , ma lo raggiungerà solo se l’angolazione della velocità iniziale è $\alpha = \frac{\pi}{4}$ .