Lagrange – L'Entropia nell'Universo può solo aumentare

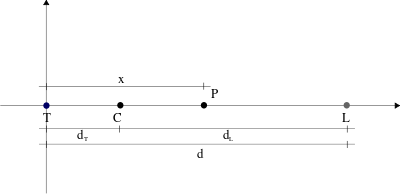
Dopo aver trovato i punti lagrangiani sulla congiungente Terra-Luna possiamo porci il problema più generale dell’esistenza di punti sul piano dell’orbita nei quali la risultante delle forze sia nulla.
Terra e Luna ruotano intorno ad un comune centro di massa $C$ , che si trova lungo la loro congiungente, ad una distanza $d_T$ dalla Terra e $d_L$ dalla Luna:

k=\frac{M_T}{M_L}

d_T=\frac{d}{1+k}

d_L=\frac{k}{1+k} d

Supponendo che il loro moto sia circolare uniforme, di periodo T, l’accelerazione centripeta della Terra e della Luna può essere espressa come:

a_T=\frac{v_T^2}{d_T}=\left(\frac{2 \pi d_T}{T}\right)^2\; \frac{1}{d_T}=\frac{4 \pi^2}{T^2}\; d_T=\frac{4 \pi^2}{T^2}\; \frac{d}{1+k}

a_L=\frac{v_L^2}{d_L}=\left(\frac{2 \pi d_L}{T}\right)^2\; \frac{1}{d_L}=\frac{4 \pi^2}{T^2}\; d_L=\frac{4 \pi^2}{T^2}\; \frac{k}{1+k} d

Dalla forza di mutua attrazione tra i due corpi è possibile ricavare una diversa espressione dell’accelerazione centripeta:

F_{T-L}=G\; \frac{M_T\;M_L}{d^2} \Rightarrow a_T=\frac{F_{T-L}}{M_T}=G\; \frac{M_L}{d^2}

Uguagliando le due espressioni:

G\; \frac{M_L}{d^2}=\frac{4 \pi^2}{T^2}\; \frac{d}{1+k} \Rightarrow \frac{4 \pi^2}{T^2} = G\; \frac{M_L}{d^3}\left(1+k\right)

Imponiamo che anche il punto $P\equiv(\rho,\theta)$ ruoti intorno al punto $C$ anch’esso con periodo T; la sua accelerazione centripeta sarà:

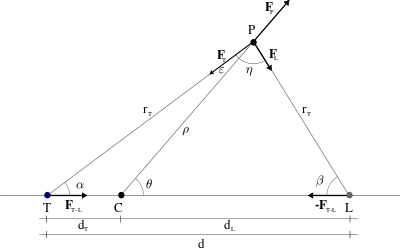
a_P=\frac{v_P^2}{\rho}=\left(\frac{2\pi\rho}{T}\right)^2\frac{1}{\rho}=\frac{4\pi^2}{T^2}\rho=G\frac{M_L}{d^3}(1+k)\rho

Il corpo nel punto P ha una massa m, che supponiamo molto più piccola di $M_T$ e $M_L$ . Le forze agenti sul punto P saranno:

F_T=G\;\frac{m\;M_T}{r_T^2}

F_L=G\;\frac{m\;M_L}{r_L^2}

F_P=m\;a_P=G\frac{m\;M_L}{d^3}(1+k)\rho

Cerchiamo i punti in cui queste forze si equilibrano. Scomponiamole lungo la direzione radiale e tangenziale.

Imponendo l’equilibrio tra le componenti tangenziali:

F_T\; \sin \varepsilon = F_L\; \sin \eta

Dalle uguaglianze:

\frac{d_L}{\sin \eta}=\frac{r_L}{\sin \theta} \Rightarrow \sin \eta=\frac{d_L}{r_L}\; \sin \theta

\frac{d_T}{\sin \varepsilon}=\frac{r_T}{\sin \theta} \Rightarrow \sin \varepsilon=\frac{d_T}{r_T}\; \sin \theta

Si ha quindi
$F_T\;\frac{d_T}{r_T}\;\sin\theta=F_L\;\frac{d_L}{r_L}\;\sin\theta \Rightarrow F_T\;\frac{d_T}{r_T}=F_L\;\frac{d_L}{r_L}$

Sostituendo si ha:
$G\;\frac{m\;M_T}{r_T^3}\;\frac{d}{1+k}=G\;\frac{m\;M_L}{r_L^3}\;\frac{k}{1+k}\;d$

quindi

r_T^3=r_L^3 \Rightarrow r_T=r_L \Rightarrow \alpha=\beta

Il punto P si trova sul vertice di un triangolo isoscele di lato $r=r_T=r_L$ .

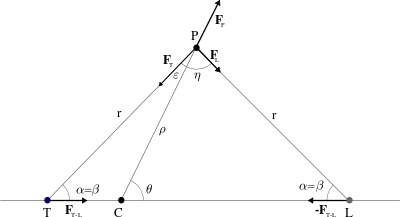
Ricerca dei punti Lagrangiani L4 e L5 al vertice di un triangolo isoscele

Nella direzione radiale, imporre l’equilibrio equivale a:

F_T \cos\varepsilon +F_L \cos \eta = F_P

\frac{d}{2}=r\; \cos \alpha \Rightarrow \cos \alpha = \frac{1}{2}\; \frac{d}{r}

\rho^2 = r^2 + d_T^2\; \cos \alpha = r^2 + \frac{d^2}{(1+k)^2}-2\; r \frac{d}{1+k}\; \frac{1}{2}\; \frac{d}{r}=r^2+\frac{d^2}{1+k}\;\left(\frac{1}{1+k}-1\right)=r^2-d^2\;\frac{k}{(1+k)^2}

d_T^2 = r^2 + \rho^2 -2\; r\; \rho \cos \varepsilon \Rightarrow \cos \varepsilon =\frac{r^2 + \rho^2 -d_T^2}{2\; r\; \rho} = \left(2\; r^2 -\frac{d^2}{1+k} \right)\; \frac{1}{2\; r\; \rho}

d_L^2 = r^2 + \rho^2 -2 r \rho\; \cos \eta \Rightarrow \cos \eta = \left(2 r^2-d^2\frac{k}{1+k}\right)\; \frac{1}{2 r \rho}

G \frac{m M_T}{r^2} \cos \varepsilon + G \frac{m M_L}{r^2} \cos \eta =G \frac{m M_L}{d^3} (1+k) \rho

\frac{k}{r^2}\; \cos \varepsilon + \frac{1}{r^2}\; \cos \eta = \frac{1+k}{d^3}\; \rho

\frac{k}{r^2}\;\left(2 r^2 -\frac{d^2}{1+k}\right)\; \frac{1}{2r\rho}+\frac{1}{r^2}\; \frac{1}{2r\rho}\left(2 r^2 -d^2 \frac{k}{1+k}\right) = \frac{1+k}{d^3}\; \rho

2 k r^2-d^2\frac{k}{1+k}+2r^2-d^2\frac{k}{1+k}=2\; \frac{1+k}{d^3}\; r^3 \rho^2

2(1+k)r^2-2 d^2 \frac{k}{1+k}=2 \frac{1+k}{d^3} r^3 \rho^2

(1+k)r^2-d^2 \frac{k}{1+k}=\frac{1+k}{d^3}\; r^3\; \left(r^2 -d^2\; \frac{k}{(1+k)^2} \right)

\frac{1+k}{d^3}\; r^5 -\frac{k}{1+k}\;\frac{r^3}{d}-(1+k)\; r^2+d^2 \frac{k}{1+k}=0

(1+k)\; r^5 -\frac{k}{1+k}\;d^2\; r^3-(1+k)\; d^3\; r^2+d^5 \frac{k}{1+k}=0

(1+k)^2\; r^5 -k\;d^2\; r^3-(1+k)^2\; d^3\; r^2+k\; d^5=0

(1+k)^2\; r^2 \left(r^3 -d^3 \right)-k d^2 \left(r^3 -d^3 \right)=0

\left((1+k)^2 r^2 -k d^2\right)\left(r^3 -d^3\right)=0

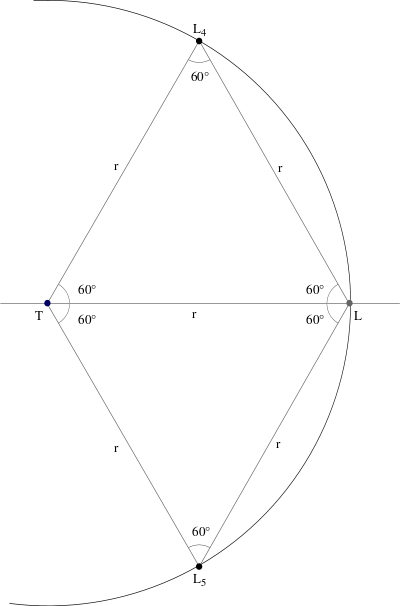
Ricerca dei punti Lagrangiani L4 e L5 al vertice di un triangolo equilatero

$r = d$ , ovvero il punto P si trova al vertice di un triangolo equilatero e $\alpha=60^\circ$ . Per simmetria di questi punti ne esistono due, e sono indicati con $L_4$ e $L_5$ .

I Punti di Lagrange sono i punti appartenenti al piano dell’orbita (della Luna per esempio, in moto rispetto alla Terra), che si muovono in modo che la configurazione spaziale Terra-Luna-Punto non cambi.

Ricerca dei punti di Lagrange L1 L2 e L3

Nel sistema Terra-Luna i due corpi ruotano intorno ad un comune centro di massa $C$ , con un moto che, per semplificare, supponiamo circolare uniforme. Le rispettive distanze della Terra e della Luna dal punto $C$ sono:

$d_T=\frac{1}{1+k}\ d$
$d_L=\frac{k}{1+k}\ d$

Dove $k$ è il rapporto $M_T/M_L$ e $d$ la distanza tra i due centri di massa.
L’accelerazione centripeta che agisce sulla Terra nel suo moto circolare uniforme rispetto al punto $C$ è pari alla forza gravitazionale dovuta dall’azione della Luna:

$a_T=\frac{v^2}{d_T}=\frac{4 \pi^2}{T^2} d_T=G \frac{M_L}{d^2} \Rightarrow \omega = \frac{4 \pi^2}{T^2}=G M_L \frac{1+k}{d^3}$ .

Un corpo di massa $m\ll\ M_T$ e $M_L$ , posto sulla retta congiungente Terra-Luna, è soggetto alle attrazioni gravitazionali di entrambi i corpi; scelto il sistema di riferimento in modo che l’origine coincida con la Terra e l’asse $x$ con la retta Terra-Luna si ha:

Forza di attrazione della Terra: $F_T=G \frac{m\ M_T}{x^2}$ , sull’asse Terra-corpo e verso diretto in direzione della Terra, quindi con il segno positivo per $x < 0$ e negativo per $x > 0$ .
Forza di attrazione della Luna: $F_L=G \frac{m\ M_L}{(d-x)^2}$ , sull’asse corpo-Luna e verso diretto in direzione della Luna, quindi con il segno positivo per $x < d$ e negativo per $x > d$ .

Tale corpo inoltre ruota intorno al punto $C$ con moto circolare uniforme, con la stessa velocità angolare $\omega$ della Terra, in modo da rimanere sull’asse $x$ , su di esso agisce una forza centripeta:

$F_C=m a_c=m \frac{v^2}{r} = m \frac{4 \pi^2 r^2}{T^2} \frac{1}{r} = \\ = m \frac{4 \pi^2}{T^2}(x-d_T)= m \omega \left(x-\frac{d}{1+k} \right)=G m \frac{M_L}{d^3}(1+k)\left(x-\frac{d}{1+k}\right)= \\ = G m M_L \left(\frac{(1+k)x}{d^3} -\frac{1}{d^2}\right)$ .

Sommando le forze che agiscono sulla massa $m$ otteniamo che l’accelerazione che essa subisce è:

a = \begin{cases} G \frac{M_T}{x^2} + G \frac{M_L}{(d-x)^2} + G M_L \left(\frac{(1+k)x}{d^3} - \frac{1}{d^2}\right) & \text{se }\; x < 0 \\ -G \frac{M_T}{x^2} + G \frac{M_L}{(d-x)^2} + G M_L \left(\frac{(1+k)x}{d^3} - \frac{1}{d^2}\right) & \text{se }\; 0 < x < d \\ -G \frac{M_T}{x^2} - G \frac{M_L}{(d-x)^2} + G M_L \left(\frac{(1+k)x}{d^3} - \frac{1}{d^2}\right) & \text{se }\; x > d \end{cases}

Cerchiamo i punti in cui tale accelerazione risulta nulla. Con una opportuna scelta delle unità di misura è possibile scrivere le seguenti equazioni:

\begin{cases} \frac{k}{x^2} + \frac{1}{(1-x)^2} + (1+k)x-1 = 0 & \text{se} \, x < 0 \\ - \frac{k}{x^2} + \frac{1}{(1-x)^2} + (1+k)x-1 = 0 & \text{se} \, 0 < x < d \\ - \frac{k}{x^2} - \frac{1}{(1-x)^2} + (1+k)x-1 = 0 & \text{se} \, x > d \end{cases}

Queste tre equazioni ammettono ciascuna una soluzione nel rispettivo insieme di definizione. Sono questi i punti di Lagrange $L_1\, \left( x < 0 \right)$ , $L_2\, \left( 0 < x < d \right)$ e $L_3\, \left( x > d \right)$ .

Nel caso del sistema Terra-Luna si ha

$M_T=5,98 \times 10^{24} kg$
$M_L=7,35 \times 10^{22} kg$

quindi $k=81,30$ . Si può applicare un qualunque metodo numerico per la ricerca degli zeri alle suddette equazioni nel rispettivo intervallo di definizione, ottenendo:

$L_1=0,849 d = 3,23 \times 10^5 km$ quindi poco prima della Luna
$L_2=1,168 d = 4,44 \times 10^5 km$ appena oltre la Luna
$L_3=0,993 d = 3,77 \times 10^5 km$ sul semiasse negativo all’incirca nella parte diametralmente opposta alla Luna.

I Punti di Lagrange $L_1$ e $L_2$ si trovano quindi in prossimità della Luna, mentre $L_3$ si trova ad una distanza pari all’incirca alla distanza Terra-Luna sul lato opposto a quest’ultima.

Tag: Lagrange

I punti di Lagrange L4 e L5

I punti di Lagrange L1, L2 e L3