Tag: tunnel

Treno a gravità

franzpizzo

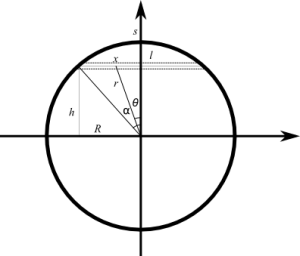
Tunnel sotterraneo
Tunnel sotterraneo
Si immagini di creare una galleria lungo una linea che congiunga due qualunque punti della sfera terrestre. Un treno che scorre lungo i binari installati lungo questo tunnel, il cui moto non sia influenzato significativamente dall’attrito, può percorrere tutta la galleria sfruttando la sola azione della gravità. Ciò si deduce dal fatto che i punti della superficie terrestre sono equipotenziali e che la forza gravitazionale è conservativa.
Sia:

  • s = 2 \alpha R \Rightarrow \alpha = \frac{s}{2 R}
  • h = R \cos \alpha = R \cos \frac{s}{2 R}
  • l = 2 R \sin \alpha = 2 R \sin \frac{s}{2 R}


    • Un corpo che si trovi all’interno di una sfera cava è soggetta alla forza di gravità esercitata dalla massa del guscio della sfera. Si dimostra che tale azione ha risultante è nulla, per cui all’interno della Terra un oggetto è sottoposto alla gravità della massa sferica che si trova al di sotto. Supponendo la densità \rho della Terra uniforme tale massa sarà
    M(r)=\rho\,\frac{4}{3}\;\pi\,r^3 = \frac{M_T}{ \frac{4}{3}\,\pi\,R_T^2 } \frac{4}{3}\,\pi\,r^3 = M_T \frac{r^3}{R_T^3}.

    Il modulo della forza esercitata dal corpo sarà quindi:

    F = G \frac{M(r)\,m}{r^2}= G \frac{M_T\,m}{R_T^3} r
    La componete verticale è annullata dalla reazione vincolare (il binario che sostiene il treno), mentre quella orizzontale sarà:

    F_x=- G\,\frac{M_T\,m}{R_T^3} r \sin \theta =- G\,\frac{M_T\,m}{R_T^3} x.

    L’equazione del moto si può scrivere quindi:

    \ddot{x} + G\,\frac{M_T}{R_T^3}=0

    che rappresenta un moto armonico di periodo T=2 \pi\,\sqrt{\frac{R_T^3}{G\,M_T}}.

    L’equazione oraria del moto avrà la forma:

    x = A \sin \left( \omega\,t + b \right)

    Con A e b costanti dipendenti dalle condizioni iniziali, mentre \omega si ricava derivando più volte l’equazione del moto:

  • \dot{x}= \omega A \cos \left( \omega\,t + b \right)
  • \ddot{x}=- {\omega}^2 A \sin \left( \omega\,t + b \right)
  • \ddot{x}=- {\omega}^2 x \rightarrow {\omega}^2=G \frac{M_T}{R_T^3}

    • Imponendo le condizioni iniziali:

  • x(0) = -\frac{l}{2} \dot{x}(0)=0
  • A \sin b = -\frac{l}{2} \omega\,A\,\cos b =0
  • A=-\frac{l}{2} B=\frac{\pi}{2}
  • A=-R_T \sin\frac{s}{2 R_T} B=\frac{\pi}{2}

    • Per cui:

    x=-R_T \sin\frac{s}{2 R_T} \sin \left( \sqrt{G\frac{M_T}{R^3}}+\frac{\pi}{2}\right)=-R_T \sin\frac{s}{2 R_T} \cos \left(\sqrt{G\frac{M_T}{R^3}} t \right)

    Il tempo di percorrenza della galleria è dato da:

    \frac{T}{2}=\frac{\pi}{\omega}=\sqrt{\frac{R_T^3}{G\; M_T}}\; \pi

    Tale valore dipende quindi solo dalla massa e dal cubo del raggio del pianeta o, in altri termini dalla sua densità e non dalla distanza tra i capi del tunnel.

    In particolare, per la Terra, un qualunque tunnel siffatto sarà percorso in un tempo indipendente dalla distanza dei due punti e sarà:

    \frac{T}{2}=\sqrt{\frac{R_T^3}{G\; M_T}}\; \pi = \sqrt{\frac{(6,37\times10^6 m)^3}{6,67 \times 10^-11 \frac{N m^2}{kg^2}\; 6\times 10^24 kg}}\; \pi = 2524 s = 42\; min\; 04\; sec

    Il treno a gravità è quindi in grado di congiungere due qualunque punti della terra in poco più di 42 minuti.