Il modello SIR permette di descrivere il diffondersi di un’epidemia in una popolazione e si applica in quei casi in cui nella popolazione \mathbb{N} si possono distinguere 3 sottoinsiemi a due a due disgiunti, composti da individui “suscettibili” \;\mathbb{S} (cioè sani e suscettibili di contagio), gli “infetti” \;\mathbb{I} (cioè in grado di trasmettere l’infezione anche se non manifestano sintomi) ed infine i “rimossi” \;\mathbb{R}, cioè tutti quelli che precedentemente erano infetti (non importa se adesso guariti o morti).
Questo modello èstato ideato da Kermack e McKendrick negli anni 20 del 20° secolo.
Si basa su queste relazioni insiemistiche ed alcune ipotesi semplificative:
- \mathbb{N}=\mathbb{S} \cup \mathbb{I} \cup \mathbb{R}
- \mathbb{S} \cap \mathbb{I} = \mathbb{S} \cap \mathbb{R} = \mathbb{I} \cap \mathbb{R} = \emptyset
Ipotesi 1
L’insieme \mathbb{N} si suppone statico (in questo modello la popolazione totale non aumenta né diminuisce, come succede in modelli più complessi per via di migrazioni e nuove nascite), ma gli insiemi \;\mathbb{S}, \;\mathbb{I} e \;\mathbb{R} variano nel tempo: avremo cioè una successione di insiemi distinti da indici crescenti. L’indice 0 corrisponde alle condizioni iniziali e i seguenti si presentano dopo un periodo fisso di tempo.
- \mathbb{S}_0, \; \mathbb{S}_1,\; \mathbb{S}_2,\; \mathbb{S}_3,\; \dots
- \mathbb{I}_0, \; \mathbb{I}_1,\; \mathbb{I}_2,\; \mathbb{I}_3,\; \dots
- \mathbb{R}_0, \; \mathbb{R}_1,\; \mathbb{R}_2,\; \mathbb{R}_3,\; \dots
Indichiamo rispettivamente con \mathcal{N} la numerosità dell’insieme \mathbb{N}, \mathcal{S}_n quella di \;\mathbb{S}_n, \mathcal{I}_n quella di \;\mathbb{I}_n e \mathcal{R}_n quella di \;\mathbb{R}_n.
Ipotesi 2
Inizialmente (quasi) tutta la popolazione è sana; gli infetti e i rimossi sono pochissimi.
\mathcal{S}_0 \approx \mathcal{N}
\mathcal{I}_0 \approx 0
\mathcal{R}_0 \approx 0
Conseguenza 1
Successivamente questi insiemi variano ma per l’ipotesi 1, per ogni n: \mathcal{N} = \mathcal{S}_n + \mathcal{I}_n + \mathcal{R}_n.
Ipotesi 3
Tra i tre insiemi avviene un continuo scambio, i suscettibili possono diventare infetti, gli infetti possono possono a loro volta passare tra i rimossi. I rimossi infine (nella nostra versione semplificata del modello) restano nel loro stato in maniera definitiva: non è possibile per loro tornare nello stato di suscettibilità ed eventualmente infettarsi nuovamente (in altri modelli i rimossi possono tornare ad essere suscettibili).
Ipotesi 4
L’infezione ha una certa probabilità di avvenire quando un suscettibile incontra un infetto. Ancora semplificando, un individuo suscettibile si incontra con qualcuno, e questi sarà infetto con probabilità \frac{\mathcal{I}}{\mathcal{N}}. Se ogni individuo suscettibile incontra k altri individui, tra di essi ci saranno quindi k \; \frac{\mathcal{I}}{\mathcal{N}} infetti.
Ogni incontro con un infetto comporta la trasmissione dell’infezione con probabilità p; molto all’ingrosso (p \; k \; \frac{\mathcal{I}}{\mathcal{N}}) rappresenta la probabilità che un individuo sano diventi infetto. Moltiplicando quest’espressione per \mathcal{S} si ottiene il totale delle persone sane che si infettano.
Sia \beta = p\;k, in un generico intervallo di tempo possiamo descrivere in questo modo la variazione dei suscettibili:
\displaystyle \Delta \mathcal{S} = - \frac{\beta}{\mathcal{N}} \; \mathcal{S} \; \mathcal{I}.
Il segno meno rende conto del fatto che il flusso di individui è in uscita da \;\mathbb{S}.
Gli infetti aumentano della stessa quantità, in quanto lo stesso flusso per loro è in ingresso, mentre diminuiscono del numero di individui che passano a rimossi.
Ipotesi 5
La variazione dei rimossi è proporzionale al numero di infetti; nell’intervallo di tempo stabilito una percentuale \gamma fissa di infetti è rimossa: \Delta \mathcal{R} = \gamma \; \mathcal{I}.
Ipotesi 6
L’insieme degli infetti ha quindi il flusso \Delta \mathcal{S} in ingresso ed il flusso \Delta \mathcal{R} in uscita, quindi la variazione degli infetti è:
Conseguenza 2
Le stesse relazioni in sintesi, che rappresentano le variazioni tra elementi consecutivi di \mathcal{S}, \mathcal{I} e \mathcal{R}:
\displaystyle \begin{cases} \Delta \mathcal{S} = - \frac{\beta}{\mathcal{N}} \; \mathcal{S} \; \mathcal{I}\\ \Delta \mathcal{I}= \frac{\beta}{\mathcal{N}} \; \mathcal{S} \; \mathcal{I} - \gamma \; \mathcal{I}\\ \Delta \mathcal{R} = \gamma \; \mathcal{I} \end{cases}
Per intervalli di tempo infinitesimi arriviamo quindi alle relazioni
\displaystyle \begin{cases} \frac{d \mathcal{S}}{dt} = - \frac{\beta}{\mathcal{N}} \; \mathcal{S} \; \mathcal{I}\\ \frac{d \mathcal{I}}{dt}= \frac{\beta}{\mathcal{N}} \; \mathcal{S} \; \mathcal{I} - \gamma \; \mathcal{I}\\ \frac{d \mathcal{R} }{dt}= \gamma \; \mathcal{I} \end{cases}
Queste ultime consistono in un sistema di equazioni differenziali, per la quale la ricerca di una soluzione analitica risulta alquanto complessa. Dal film del 2016, Il diritto di contare (Hidden figures), ci arriva questo suggerimento:
Hidden figures, 2016 – Il metodo di Eluero
Quindi risolviamo le equazioni numericamente con il metodo di Eulero. Per \mathcal{N}=3000, assegnando le condizioni iniziali coerenti con l’Ipotesi 2:
\begin{cases} \mathcal{S}(0) = 2998 \\ \mathcal{I}(0) = 1 \\ \mathcal{R}(0) = 1 \end{cases}
e assegnando un valore parametri \beta=1,3 e \gamma=1,1 basta un foglio di LibreOffice Calc per ottenere
| \mathcal{n} | \mathcal{S} | \mathcal{I} | \mathcal{R} |
|---|---|---|---|
| 0 | 2998 | 1 | 1 |
| 1 | 2996,70086666667 | 1,29913333333333 | 2 |
| 2 | 2995,0138506061 | 1,68701606056341 | 3,29913333333333 |
| 3 | 2992,82437480348 | 2,18947580261902 | 4,98614939389674 |
| 4 | 2989,98486429843 | 2,83951050505227 | 7,17562519651576 |
| 5 | 2986,30582381118 | 3,67904048725316 | 10,015135701568 |
| 6 | 2981,54490313016 | 4,7609206810192 | 13,6941761888212 |
| 7 | 2975,39378032086 | 6,15112280930323 | 18,4550968698404 |
| 8 | 2967,46290821638 | 7,93087210447592 | 24,6062196791436 |
| 9 | 2957,26459506978 | 10,1983131465975 | 32,5370917836195 |
| 10 | 2944,19564723071 | 13,0689478390759 | 42,735404930217 |
| 11 | 2927,52204684931 | 16,6736003814 | 55,8043527692928 |
| 12 | 2906,37003600532 | 21,1520108439915 | 72,4779531506928 |
| 13 | 2879,73062211408 | 26,6394138912358 | 93,6299639946843 |
| 14 | 2846,48774320772 | 33,2428789063639 | 120,26937788592 |
| 15 | 2805,48338268682 | 41,0043605208914 | 153,512256792284 |
| 16 | 2755,63399346123 | 49,8493892255929 | 194,516617313175 |
| 17 | 2696,10843580979 | 59,5255576514403 | 244,366006538768 |
| 18 | … | … | … |
Considerazione
Dal passo 1 in avanti otteniamo dei valori decimali per le numerosità, anche se gli insiemi sono discreti, pertanto ci aspettiamo solo valori interi: non ci possono essere 1,3 infetti in una popolazione. Come si interpretano questi dati? Ebbene dobbiamo tenere conto che quello che stiamo calcolando ha un valore probabilistico. Immaginiamo di avere decine o centinaia di insiemi di popolazioni tutte di dimensione \mathcal{N}=3000. In ognuna di esse, a ciascun passo, si conteranno un numero intero di sani, infetti e rimossi. Ad esempio in alcune popolazioni potrebbero esserci 1 infetto, in altre 2, in altre anche 3 o più. La media degli infetti tra tutte le popolazioni sarà decimale.
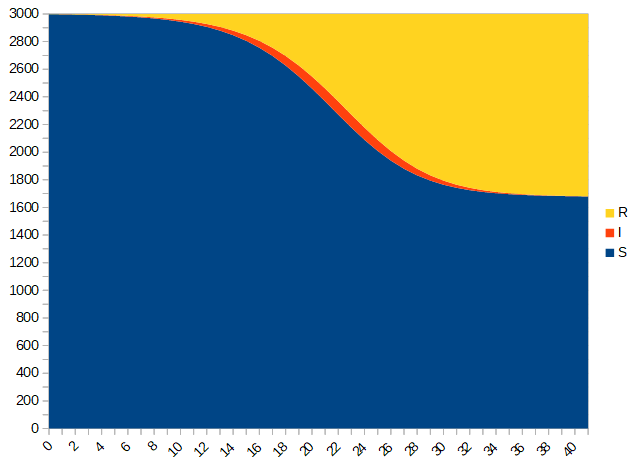
Produciamo anche un grafico di tali sequenze numeriche:
Si tratta di un andamento verosimile: all’inizio tutta la popolazione è sana (in blu), ma i sani diminuiscono rapidamente; gli infetti (in rosso) crescono ma numericamente sono sempre in quantità contenuta, dal momento che si spostano rapidamente tra i rimossi (guariscono o muoiono), mentre i rimossi (in giallo) aumentano.
La diminuzione dei sani però inizia a rallentare fino a fermarsi: il numero di sani e dei rimossi si stabilizzano intorno ad alcuni valori: si verifica ciò che in matematica si definisce asintoto. Il numero di sani infatti non scende oltre le 1676 unità, si annulla il numero di infetti, mentre i rimossi si attestano definitivamente intorno ai 1324.
Tale fenomeno si interpreta immaginando che raggiunto una certa soglia di rimossi l’infezione non può diffondersi, dal momento che nella relazione \frac{d \mathcal{I}}{dt}= \frac{\beta}{\mathcal{N}} \; \mathcal{S} \; \mathcal{I} - \gamma \; \mathcal{I} il numero di sani è inferiore rispetto all’inizio e fornisce sempre meno contributo all’incremento di \mathcal{I}. Il punto critico è rappresentato dal momento in cui \frac{\beta}{\mathcal{N}} \; \mathcal{S} \; \mathcal{I} = \gamma \; \mathcal{I}; da quel momento il numero di infetti inizia a diminuire fino ad annullarsi.
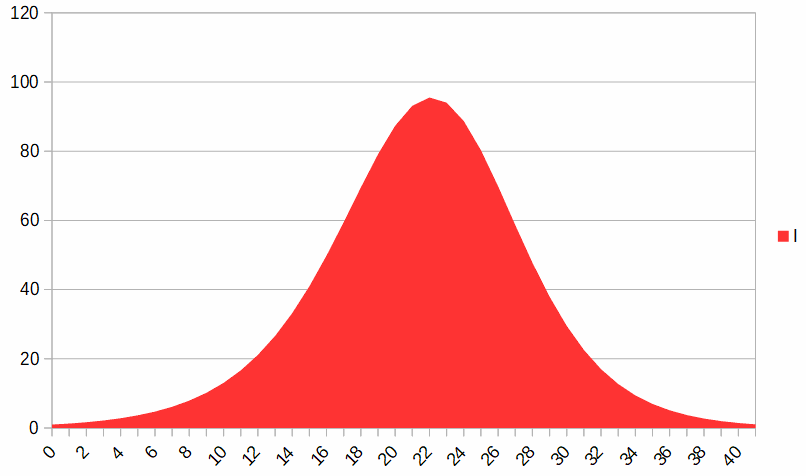
Da questo grafico si comprende l’andamento del numero di infetti; nel caso in esame il picco è intorno ai 90 infetti. Volendo approfondire l’analisi, consideriamo il rapporto \frac{d\mathcal{I}}{d\mathcal{S}} che risulta in maniera immediata corrispondere a:
\displaystyle \frac{d\mathcal{I}}{d\mathcal{S}}=\frac{\gamma}{\beta} \frac{N}{S}-1Definendo R_0 = \frac{\beta}{\gamma}, otteniamo
\displaystyle \frac{d\mathcal{I}}{d\mathcal{S}}=\frac{\mathcal{N}}{R_0} \frac{1}{\mathcal{S}}-1Ciò significa che il numero di infetti avrà un massimo e smetterà di crescere per \frac{\mathcal{N}}{R_0} \frac{1}{\mathcal{S}}-1 = 0 ovvero per \mathcal{S} =\frac{\mathcal{N}}{R_0}, e quindi nel nostro esempio \mathcal{S} =\frac{3000}{1,3} \approx 2308.
La relazione analitica che lega \mathcal{I} e \mathcal{S} si determina risolvendo l’integrale:
\displaystyle \mathcal{I}=\int{(\frac{\mathcal{N}}{R_0} \frac{1}{\mathcal{S}}-1 )} d\mathcal{S} = \frac{\mathcal{N}}{R_0} \ln{\mathcal{S}}-\mathcal{S} + c.
dove la costante di integrazione c si determina dalle condizioni di contorno: \mathcal{I}(\mathcal{N})=0, ovvero \frac{\mathcal{N}}{R_0} \ln{\mathcal{N}}-\mathcal{N} + c = 0, quindi c = \mathcal{N} - \frac{\mathcal{N}}{R_0} \ln{\mathcal{N}}. In definitiva la relazione analitica che lega il numero di sani e il numero di infetti è
\displaystyle \mathcal{I}(\mathcal{S})= \frac{\mathcal{N}}{R_0} \ln{\mathcal{S}}-\mathcal{S} + \mathcal{N} - \frac{\mathcal{N}}{R_0} \ln{\mathcal{N}}.
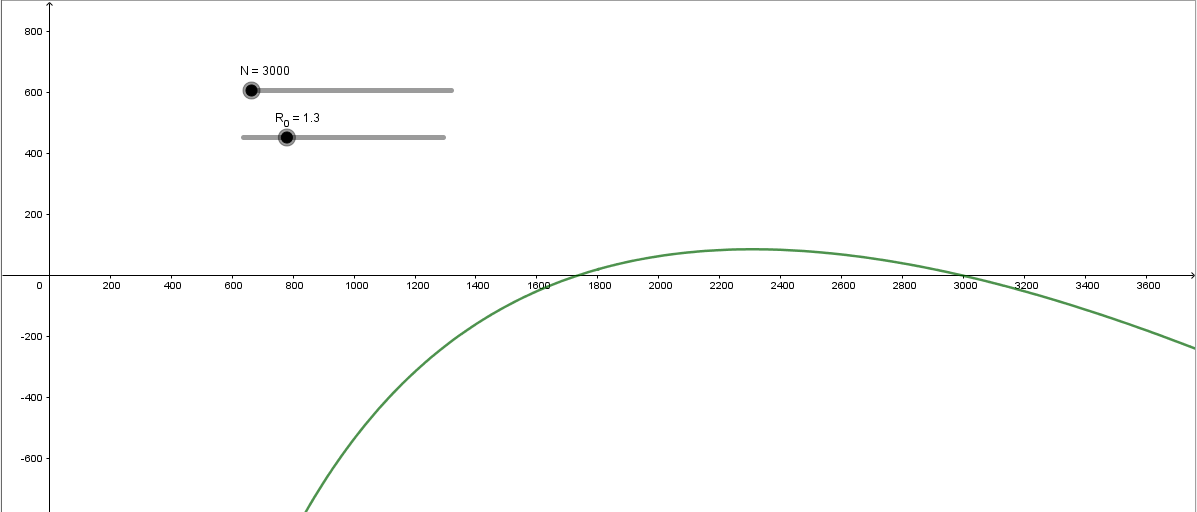
Il cui grafico, per i valori in esame, disegnato in GeoGebra è il seguente:
dove solo i valori positivi di \mathcal{I} hanno significato.
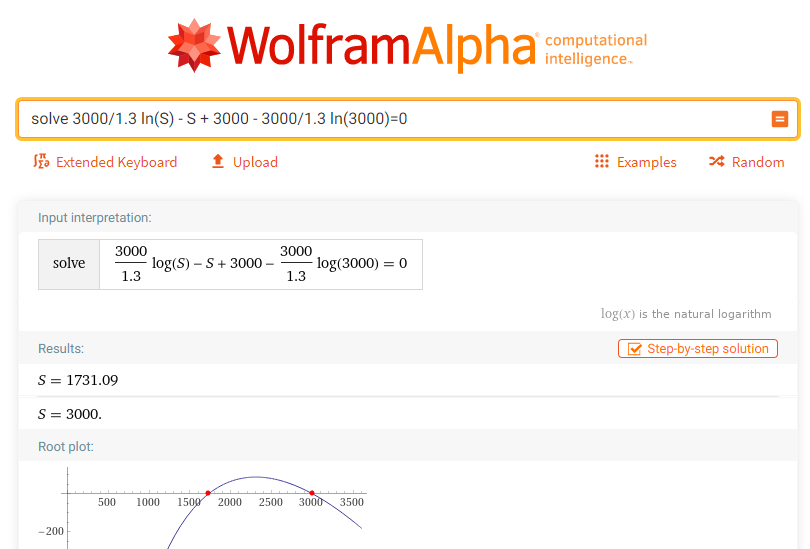
Interpretiamo questo grafico: ad un estremo il suo valore è \mathcal{S}=3000, ovvero la condizione iniziale. La curva tocca l’asse delle ascisse anche in un altro punto, che si può determinare numericamente. Si possono applicare diversi metodi numerici o trovare la soluzione tramite GeoGebra; questa volta però andiamo su Wolfram Alpha, ottenendo:
Il numero di infetti sarà quindi in totale 1731 (una stima in linea con il metodo di Eulero applicato sopra, ma certamente più precisa, dal momento che il metodo comporta delle approssimazioni). L’insieme degli infetti si svuota e alla fine questi 1731 saranno tutti rimossi. Di conseguenza alla fine i sani saranno \mathcal{S}=3000 - 1731=1269. Quando il numero di sani raggiunge questa quota l’infezione si spegne da sola perché non trova spazio per diffondersi; si parla in questo caso di “immunità di gregge“.
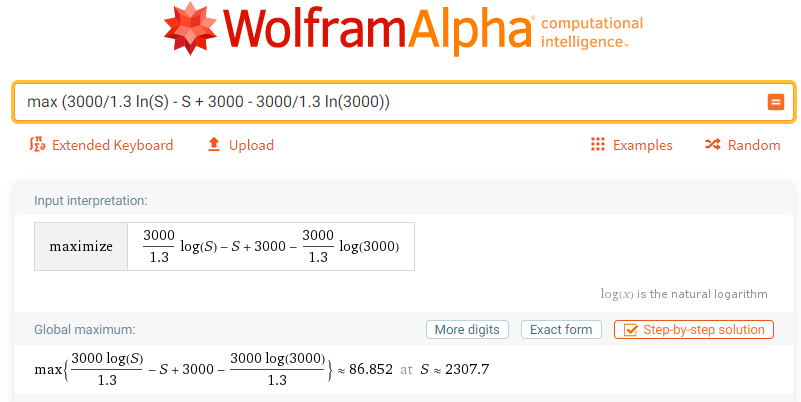
Poiché il massimo degli infetti si avrà per \mathcal{S} =\frac{\mathcal{N}}{R_0}, calcoliamo \mathcal{I}(\frac{\mathcal{N}}{R_0})= \mathcal{N} - \frac{\mathcal{N}}{R_0} - \mathcal{N} \ln(R_0), che nel caso del nostro esempio corrisponde a \mathcal{I} \approx 87. Infatti buttando la nostra formula in pasto a Wolfram otteniamo:
Da tutto questo preambolo matematico possiamo dedurre che:
Date le condizioni di contorno \mathcal{N} e R_0, l’andamento dell’infezione è, per grandi numeri, deterministica, così come in cinematica lo è il moto di un proiettile. A partire da questi due valori è possibile determinare
- il numero totale di persone che si infetteranno, e in base alla mortalità dell’infezione anche il numero totale di morti
- il massimo numero di infetti, e quando si verifica
- stabilire quando l’infezione comincia a calare
- il momento in cui si raggiunge l’immunità di gregge e l’infezione scompare autonomamente
Esempio del covid-19 in Lombardia, 10 milioni di persone e in un fase (fonte ministero della salute)R_0 \approx 3, applicando lo stesso modello in totale il numero di infetti sarebbe stato intorno ai 9.400.000, con una punta di 3.000.000 di infetti contemporaneamente.
L’unica e reale soluzione per fermare qualunque infezione è raggiungere l’immunità di gregge, e ciò si può fare in due modi:
- trovare il modo di far transitare artificialmente il maggior numero di individui della popolazione sana tra i rimossi con la vaccinazione
- lasciare che l’infezione faccia il suo corso diffondendosi tra la popolazione fino a fermarsi da sola
Nel caso del covid-19, dal momento che la prima opzione non era disponibile, c’è stato chi si è orientato sulla seconda opzione, si tratta dell’asse Trump-Bolsonaro-Putin-Johnson. Come è andata? Bene direi…
Alternative? Anche se si può definire solo un metodo per “tamponare”, ha il vantaggio di funzionare: diminuire il più possibile il fattore R_0.
Ricordando la definizione R_0 = \frac{\beta}{\gamma}, possiamo aumentare \gamma, ovvero il fattore di guarigione degli infetti, ottenendo come effetto secondario una riduzione di R_0 e quindi della diffusione dell’epidemia. Ma l’aumento di \gamma ha dei limiti, ci si può impegnare a guarire più persone e più velocemente ma non sarà possibile migliorare moltissimo questo parametro. Meglio quindi provare ad aumentare \beta.
Il parametro \beta, per l’ipotesi 4 è dato da due fattori: \beta = p \;k. la probabilità che nell’incontro con un infetto ci si possa contagiare rappresentato da p e k il numero di incontri che compie mediamente una persona: come ridurre questi due fattori?
È a questo punto che entra in gioco l’eroe di questa storia, l’unico che è in grado di capire tutto quello che è scritto sopra ed altro ancora e che ha risolto in maniera brillante la situazione: il sindaco, presidente, commendatore, ministro, eccellenza, onorevole, bersagliere Vincenzo De Luca.

Una figura che rispetto ai vari Trump, Bolsonaro, Putin e Johnson spicca per ardire, acume politico professionalità, determinazione.
Nessuno saprà mai com’è andata ma si può immaginare che la scena non sia stata molto diversa da questa:
A Beautiful Mind (film biografico ispirato alla vita del matematico John Nash), film del 2001, la scena del Pentagono
A questo punto l’Eroico Presidente interviene con una serie di ordinanze a partire dal 26 febbraio e nei giorni successivi, che decretano il fermo totale di tutta la Campania: nessuno entra o esce più di casa, niente bar, niente barbiere, neppure una passeggiata, al limite se hai il cane lo puoi portare fuori, ma solo appena fuori casa tua.
E per chi sgarra? La risposta a tutto è: il lanciafiamme! Il parametro k passa immediatamente a zero!
20 marzo 2020 – De Luca che minaccia l’intervento dei Carabinieri con il lanciafiamme
Ma non basta, ci vogliono le mascherine quando si va a fare la spesa; ed ecco l’altra idea geniale: le mascherine obbligatorie, sempre, ovunque. Premesso che non si esce di casa, se dopo tre giorni che hai finito il cibo hai fame puoi andare a comprarlo, ma devi avere la mascherina e anche p scende a picco.
27 marzo 2020 – De Luca mostra le speciali mascherine da Bugs Bunny
Ed è un successo: la Campania è salva, grazie a De Luca, che adesso giunge al massimo dei consensi, e a settembre andrà all’incasso. Sì, perché a settembre ci saranno le elezioni regionali e si prevede che De Luca debba raccogliere voti a mani basse. Ben per lui!
Ma si affaccia all’orizzonte un cupo e inquietante fenomeno. Le liste elettorali che appoggiano il Presidente si stanno gonfiando in maniera smisurata, si è verificata una convergenza inaspettata verso le liste che appoggiano De Luca. Analogamente a quanto avviene alla popolazione degli infetti nel modello SIR, anche in questo caso la crescita dei transfughi è esponenziale: sono tutti passati dall’altra parte!
I male informati stanno diffondendo la voce che, fatti i conti sul numero di voti che andranno a De Luca, molti candidati si sono orientati verso la lista vincente e ciò a prescindere dal loro passato, buttandosi alle spalle militanze decennali, orientamenti consolidati e questo solo per una poltrona: basse insinuazioni.
Le convergenze, o per meglio dire le conversioni sono molte e di alto rango e De Luca di certo non disprezza il peso elettorale dei nuovi arrivati, conosciamo la sua magnanimità e il suo spirito di accoglienza. Ed allora vediamo salire sul carro ben note personalità, che oltre a portare la loro presenza si accodano con tutto il loro carrozzone. Qualcun altro si sentirebbe “imbarazzato” da tanto inaspettato affetto che lo circonda, da tutte le persone che ti appoggiano, dal tipo di persone che ti appoggiano, ma lui no, raccoglie da qualunque parte: è il modello SIR bellezza! E tu non puoi farci niente! Niente!