Un cavo vincolato ai suoi estremi a due punti fissi e soggetto alla sola forza peso assume una configurazione caratteristica simile ad una parabola; tale curva viene detta catenaria.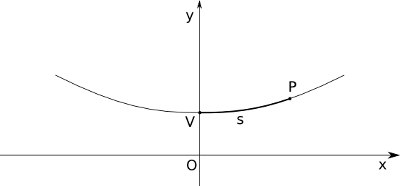
La curva “assomiglia” ad una parabola in quanto ha nella sua estremità inferiore un vertice, è concava verso l’alto e simmetrica rispetto ad un asse passante per il vertice.
Consideriamo un sistema di riferimento in cui l’asse delle ordinate coincide con l’asse di simmetria, orientato nel verso della concavità.
A partire dal vertice muoviamoci lungo la curva percorrendo uno dei suoi rami, per esempio quello di ascissa positiva, per un tratto di lunghezza s fino al punto P.
Le coordinate del punto P dipendono dal tratto s percorso:
Affinché sussista l’equilibrio statico la risultante delle forze che agiscono su un qualunque tratto \Delta\,s del cavo è nulla. Su \Delta\,s agisce una forza peso che dipende dalla densità lineare \lambda del cavo, di modulo \Delta\,F = \lambda\;g\;\Delta\,s, diretta verso il basso.
Gli estremi di \Delta\,s sono invece soggetti alle tensioni \vec {T}(s) e \vec {T}(s + \Delta\,s) la cui risultante è \Delta\,\vec{T} = \vec{T} (s + \Delta\,s) - \vec{T}(s). Per la staticità della configurazione la risultante delle forze a cui è soggetto il segmento \Delta\,s è nulla, quindi \Delta\,\vec{T}= \lambda\;h\;\Delta\,s\;\hat j, dove \hat j è il versore dell’asse delle ordinate.
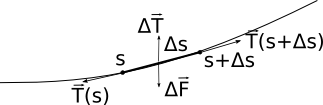
Passando alle componenti
Poiché queste uguaglianze valgono anche per un tratto di curva infinitesimo ds abbiamo
\begin{cases}d T_x = 0\\ d T_y = \lambda\;g\;d s\end{cases} \Rightarrow \\{ \begin{cases} & \int_{T_x (0)}^{T_x (s)} d \tau = c\\ & \int_{T_y (0)}^{T_y (s)} d \tau = \int_{0}^{s} g \lambda d \sigma\end{cases} \Rightarrow \\ \begin{cases} T_x (s) - T_x (0) = c\\ T_y (s) - T_y (0) = g\;\lambda\;s \end{cases} }Quindi T_x (s) = T_x (0) + c e dal momento che T_x (0) = T_x (0) + c allora c = 0, cioè la componente orizzontale della tensione è costante su tutto il ramo della corda di ascissa positiva, ponendo perciò T_0 = T_x (0), avremo T_x (s) = T_0 lungo tutta la corda.
D’altra parte T_y, la componente verticale della tensione, è dovuta al peso del cavo di lunghezza s compreso tra il vertice e il punto P, quindi si ha T_y(0) = 0. Abbiamo infine
che può essere scritta come
\begin{cases} T \frac{dx}{ds} = T_0\\ T \frac{dy}{ds} = g\;\lambda\;s \end{cases}avendo considerato le componenti \frac{dx}{ds} e \frac{dy}{ds} del versore della tangente alla curva e T il modulo della tensione \vec{T}.
Dalle due equazioni otteniamo
T \frac{dy}{ds} \frac{1}{T} \frac{dx}{ds} = \frac{g \lambda}{T_0} \Rightarrow \frac{dy}{dx}=\frac{g \lambda}{T_0} s e ponendo a=\frac{T_0}{g \lambda} \Rightarrow \frac{dy}{dx}=\frac{s}{a}.
Inoltre poiché
(ds)^2 = (dx)^2 + (dy)^2 \Rightarrow \\ ds = \sqrt{1 + \left ( \frac{dy}{dx} \right )^2 } dx \Rightarrow \\ ds = \sqrt{1 + \left ( \frac{s}{a} \right )^2 } dx \Rightarrow \Rightarrow dx = \frac{ds}{\sqrt{1 + \left ( \frac{s}{a} \right )^2 } }\Rightarrow \\ dx = a \frac {d \left ( \frac{s}{a} \right )}{\sqrt{1 + \left ( \frac{s}{a} \right )^2 }}integrando
\int_{0}{x} d \xi = a \int_{0}{\frac{a}{s}} \frac{dt}{\sqrt{1 + t^2}} \Rightarrow \\ x=a \left [ log( t + \sqrt{1 + t^2} ) \right ]_0^\frac{s}{a} \Rightarrow \Rightarrow x = a\;log \left ( \frac{s}{a} + \sqrt{1 + \left ( \frac{s}{a}\right )^2} ) \right ) \Rightarrow \\ \frac{x}{a}= log \left ( \frac{s}{a} + \sqrt{1 + \left ( \frac{s}{a}\right )^2} ) \right )Quest’ultima relazione può essere invertita scrivendo s in funzione di x:
e^{ \frac{x}{a} } = \frac{s}{a} + \sqrt{1+ \left ( {\frac{s}{a}} \right )^2} \Rightarrow e^{2 \frac{x}{a} } - 2\; \frac{s}{a}\; e^{ \frac{x}{a} } + \left ( {\frac{s}{a}} \right )^2 = 1 + \left ( {\frac{s}{a}} \right )^2 \Rightarrow\Rightarrow e^{\frac{x}{a} } - 1 = 2\;{\frac{s}{a}}\; e^{\frac{x}{a} } \Rightarrow \\ 2\;{\frac{s}{a}} = e^{\frac{x}{a} } - e^{- {\frac{x}{a}} } \Rightarrow \\s = a\; \frac{{e^{\frac{x}{a} } - e^{-\frac{x}{a}} }}{2}
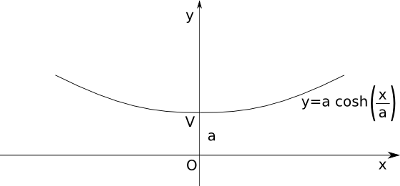
Cioè s = a\;\sinh \left ( \frac{x}{a} \right ).
Quindi \frac{dy}{dx} = \frac{s}{a} \Rightarrow \frac{dy}{dx} = \sinh \left ( \frac{x}{a} \right ) \Rightarrow y = a\;\cosh \left ( \frac{x}{a} \right ) + c dove c si può scegliere liberamente traslando in maniera opportuna il sistema di coordinate. Imponendo y(0)=a si ha c=0 e pertanto y = a\;\cosh \left ( \frac{x}{a} \right ).
Diverso è il caso di un cavo soggetto al un carico uniforme p e per il quale il carico dovuto al proprio peso è trascurabile. Ciò si verifica nei classici ponti sospesi, in cui il cavo funge da struttura portante.
La forza verticale che agisce su ogni tratto \Delta\,s è in questo caso \Delta\,\vec{F}= p\;\Delta\,x\;\hat jper cui possiamo riscrivere le equazioni della tensione in questo modo
da cui
y = \frac{p}{2\;T_0}\;x^2 + c.
Scegliendo opportunamente il sistema di riferimento in modo che y(0)=0 si ha c=0 e quindi y = \frac{p}{2\;T_0}\;x^2 che si riconosce essere l’equazione della parabola.