La brachistocrona

Il problema della brachistocrona consiste nel trovare la particolare traiettoria che un corpo, soggetto alla sola forza peso, deve compiere nel passare da un punto A ad un punto B posto ad una quota più bassa, che sia tale da minimizzare il tempo di percorrenza.

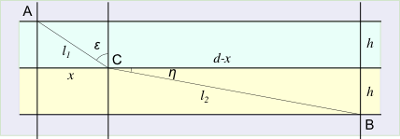
La ricerca di questa curva può avvenire notando l’analogia con quanto avviene per la rifrazione della luce. Nel passaggio da un mezzo all’altro la luce varia la sua velocità e il percorso che compie nell’unire due punti è quello che gli permette di impiegare meno tempo. I punti A e B si trovano agli estremi di due strati di materiali diversi e di uguale spessore h. La luce attraverserà la linea di separazione in un punto C da determinare. Nei due strati la luce ha velocità rispettivamente

v_1 e v_2 e percorre i tratti l_1=\sqrt{h^2 + x^2} e l_2=\sqrt{h^2 + (d-x)^2} con tempi di percorrenza
t_1 = \frac{l_1}{v_1} = \frac{\sqrt{h^2 + x^2}}{v_1} e t_2=\frac{l_2}{v_2}=\frac{\sqrt{h^2 + (d-x)^2}}{v_2}.
Il tempo totale di percorrenza risulta quindi
t = t_1 + t_2 = \frac{\sqrt{h^2 + x^2}}{v_1} + \frac{\sqrt{h^2 + (d-x)^2}}{v_2}.
Scegliamo la posizione del punto C in modo da minimizzare il tempo di percorrenza. Il punto di minimo dell’espressione del tempo deve avere necessariamente derivata nulla:

\frac{dt}{dx} = \frac{1}{2} \frac{1}{v_1} \frac{2 x}{\sqrt{h^2 + x^2}} + \frac{1}{2} \frac{1}{v_2} \frac{-2 (d-x) }{\sqrt{h^2 + (d-x)^2}}=
= \frac{x}{v_1 \sqrt{h^2 + x^2}}-\frac{d-x}{v_2 \sqrt{h^2 + (d-x)^2}} = \frac{x}{l_1}-\frac{d-x }{v_2 l_2} = \frac{\sin \varepsilon }{v_1}-\frac{\sin \eta }{v_2} = 0

Dove con \varepsilon e \eta abbiamo indicato gli angoli di incidenza e di rifrazione dispetto alla normale alla superficie di separazione. Il punto C è determinato dalla soluzione della precedente equazione, inoltre si ha
\frac{\sin \varepsilon }{v_1} = \frac{\sin \eta }{v_2} = \frac{1}{k}
con k una opportuna costante.

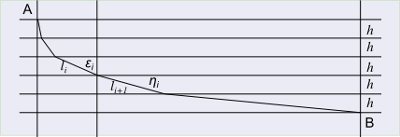
Si può generalizzare questo risultato applicando più volte ad una successione di strati contigui di uguale spessore e di materiali diversi. Nello strati i-esimo la luce percorre il tratto l_i
ad una velocità v_i e resta determinato il punto di passaggio x_i tra ciascuno strato. Il tempo totale impiegato per passare dal punto A al punto B è dato da:

t=t_1+t_2+\ldots+t_n=\frac{l_1}{v_1}+\frac{l_2}{v_2}+\ldots+\frac{l_n}{v_n}.

Quando l’ampiezza degli strati tende a zero e il loro numero tende all’infinito, la successione di tratti rettilinei tende ad una curva. Poiché

\sin \varepsilon_i = v_i \frac{\sin \eta_i}{v_{i+1}} allora \sin \varepsilon_i sarà tanto piccolo quanto più v_i è piccolo e quindi se la velocità nel primo tratto tende a zero allora \varepsilon_i tende a zero, cioè la direzione iniziale tende alla verticale. Allo stesso modo, dal momento che \sin \eta_{i+1} = v_{i+1} \frac{\sin \varepsilon_i}{v_i} allora \sin \eta_{i+1} crescerà al crescere di v_{i+1} e poiché il massimo della funzione seno si ha per \frac{\pi}{2}, la velocità massima si raggiunge quando il moto è orizzontale.

Applichiamo questo risultato al caso di un corpo che transita dal punto A al punto B e cerchiamo la traiettoria che ottimizzi il tempo di percorrenza.
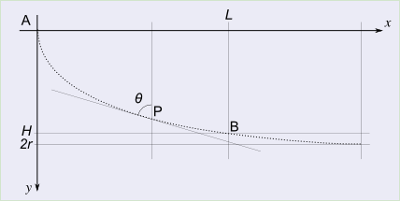
Consideriamo un sistema di riferimento con origine coincidente con il punto A e l’asse delle ordinate orientato verso il basso: A(0,0) e B(L,H).

L’energia totale di un corpo soggetto alla forza peso è
E= \frac{1}{2} m v^2 + m g y.

Tale quantità è costante dal momento che non agiscono forze non conservative inoltre imponendo la condizione iniziale v_A=0

E_A=0 \Rightarrow \frac{1}{2} m v^2 + m g y = 0

e quindi v^2 = 2 g y.

Sia \theta l’angolo che la tangente alla traiettoria forma con la verticale, poiché

\frac{\sin \theta}{v} = \frac{1}{k} costante allora

v^2 \sin^2 \theta = k^2 \Rightarrow \frac{2 g y}{\sin^2 \theta} = k^2

abbiamo y= \frac{k^2}{2 g} \sin^2 \theta.

L’angolo \theta tende a \frac{\pi}{2}.

Indichiamo invece con 2 r l’ordinata relativa alla massima velocità; avremo 2 r = \frac{k^2}{2 g} \sin \frac{\pi}{2} = \frac{k^2}{2 g}
e quindi k^2 = 4 g r.

Sostituiamo il valore di k^2 nell’espressione dell’ordinata: y=\frac{4 g r}{2 g} \sin^2 \theta = 2 r \sin^2 \theta.
Derivando quest’ultima espressione rispetto a \theta:

\frac{dy}{d\theta}=2 r \cdot 2 \sin \theta \cos \theta = 2 r \sin 2 \theta.

Poiché

\frac{dx}{dy}=\tan \theta \Rightarrow \frac{dx}{d\theta}=\frac{dx}{dy}\frac{dy}{d\theta} = \tan \theta \cdot 4 r \sin \theta \cos \theta =
=\frac{\sin \theta}{\cos \theta} \cdot 4 r \sin \theta \cos \theta = 4 r \sin^2 \theta = 2 r (1-\cos 2 \theta)

Quindi

\begin{cases}\frac{dx}{d\theta} = 2 r ( 1-\cos 2\theta ) \\ \frac{dy}{d\theta} = 2 r \sin 2\theta\end{cases}\Rightarrow\begin{cases}x = r ( 2 \theta-\sin 2\theta ) + c_1 \\ y = -r \cos 2 \theta + c_2\end{cases}

dove c_1 e c_2 sono determinate a partire dalle condizioni iniziali. È stato supposto che il corpo sia inizialmente fermo in A e quindi il suo moto inizia nella direzione verticale: \theta_A = 0

\begin{cases}0 = r ( 0-\sin 0 ) + c_1\\ 0 = -r \cos 0 + c_2 \end{cases} \Rightarrow \begin{cases} c_1 = 0\\ c_2 = r \end{cases} .

La curva cercata si esprime in forma parametrica come

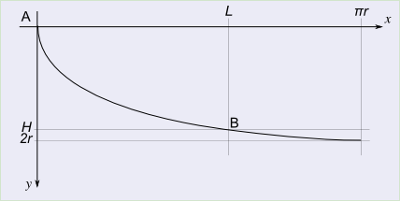
\begin{cases} x = r ( 2 \theta-\sin 2\theta ) \\ y = r ( 1-\cos 2 \theta ) \end{cases}

Si riconosce che tale curva rappresenta una cicloide ossia la curva descritta da un punto su una circonferenza di raggio r quando questi viene fatto rotolare.

Deriviamo queste ultime espressioni rispetto al tempo:

\begin{cases} \frac{dx}{dt} = \frac{dx}{d\theta} \frac{d\theta}{dt} = r ( 2 \theta-\sin 2\theta ) \dot \theta\\ \frac{dy}{dt} = \frac{dy}{d\theta} \frac{d\theta}{dt} = 2 r ( \sin 2\theta ) \dot \theta \end{cases}

Possiamo ricavare l’espressione della velocità del corpo rispetto al parametro \theta.

v^2 = \left( \frac{dx}{dt} \right)^2 + \left( \frac{dy}{dt} \right)^2 = 4 r \left [ ( 1-\cos 2 \theta )^2 + (\sin 2 \theta)^2 \right] \dot \theta^2 =
= 4 r ( 1-2 \cos 2 \theta + \cos^2 2 \theta + \sin^2 2 \theta ) \dot \theta^2 =
= 8 r^2 ( 1-\cos 2 \theta ) \dot \theta^2 = 16 r^2 ( \sin^2 \theta ) \dot \theta^2

Invertiamo tale relazione ricavando \dot \theta:

\dot \theta^2 = \frac {v^2}{16 r^2 \sin^2 \theta} = \frac{k}{16 r^2} = \frac{4 g r }{16 r^2} = \frac{g}{4 r}<br /> \Rightarrow \dot \theta = \frac{1}{2} \sqrt{\frac{g}{r}}

e integrando, e tenendo conto delle condizioni iniziali \theta_A = 0:

\theta = \int \frac{1}{2} \sqrt{\frac{g}{r}} \, dt = \frac{1}{2} \sqrt{\frac{g}{r}} t

Il tempo totale T impiegato per raggiungere il punto più basso, cioè quando
\theta = \frac{\pi}{2},
è dato dalla soluzione dall’equazione
\frac{\pi}{2} = \frac{1}{2} \sqrt{\frac{g}{r}} T \Rightarrow T = \pi \sqrt{\frac{r}{g}}

Poiché l’espressione parametrica della curva si può scrivere come

\begin{cases} x = r ( \sqrt{\frac{g}{r}} t-\sin \sqrt{\frac{g}{r}} t ) \\ y = r ( 1-\cos \sqrt{\frac{g}{r}} t )\end{cases}

Al tempo T = \pi \sqrt{\frac{r}{g}} il corpo si troverà nel punto

\begin{cases} x = r ( \pi-\sin \pi ) \\ y = r ( 1-\cos \pi ) \end{cases} \Rightarrow \begin{cases} x = \pi r \\ y = 2 r \end{cases} .